3.4.2. Motion Estimation
New image frames can be created from existing ones through temporal interpolation. Unlike spatial interpolation, temporal interpolation requires a large amount of storage. Therefore a new frame is usually created from two adjacent frames, one in the past and one in the future relative to the frame being created.
The simplest method, often used in practice, is the zero-order hold method, in which a new frame is created by repeating the existing frame which is closest in time. In transforming a 24 frames/sec motion picture to a 60 fields/sec NTSC signal, three consecutive fields are created from a single motion picture frame, and the next two consecutive fields are created from the next motion picture frame. This process is repeated for the entire motion picture. This is known as the 3:2 pull-down method. For most scenes without large global motion, the results are quite good. If there is large global motion, however, zero-order hold temporal interpolation can cause noticeable jerkiness of motion. One method to improve the performance of temporal interpolation is through motion compensation.
A motion picture or television broadcast is a sequence of still frames that are displayed in rapid succession. The frame rate necessary to achieve proper motion rendition is usually high enough to ensure a great deal of temporal redundancy among adjacent frames. Much of the variation in intensity from one frame to the next is due to object motion. The process of determining the movement of objects within a sequence of image frames is known as motion estimation. Processing images accounting for the presence of motion is called motion-compensated image processing.
Motion-compensated image processing has a variety of applications. One application is image interpolation. By estimating motion parameters, we can create a new frame between two adjacent existing frames. The application of motion-compensated processing to image interpolation is discussed in the next section. Another application is image restoration. If we can estimate the motion parameters and identify regions in different frames where image intensities are expected to be the same or similar, temporal filtering can be performed in those regions. Application to image restoration is discussed in Chapter 3. Motion-compensated image processing can also be applied to image coding. By predicting the intensity of the current frame from the previous frames, we can limit our coding to the difference in intensities between the current frame and the predicted current frame. In addition, we may be able to discard some frames and reconstruct the discarded frames through interpolation from the coded frames. Application to image coding is discussed in Chapter 4.
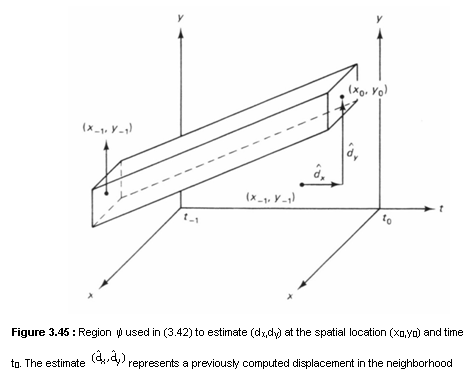
The motion estimation problem we consider here is the translational motion of objects. Let f(x,y,t-1) and f(x,y,t0) denote the image intensity at times t and t0, respectively. We will refer to f(x,y,t-1) and f(x,y,t0) as the past and current frame. We assume that
f(x,y,t0)=f(x - dx,y - dy, t-1) (3.29)
where dx and dy, are the horizontal and vertical displacement between t and t0. An example of f(x,y,t-1) and f(x,y,t0) which satisfy (3.29) is shown in Figure 3.43. If we assume uniform motion between t-1 and t0,
f(x,y,t)=f(x - vx(t-t-1),y – vy(t-t-1), t-1), t-1 £ t £ t0 (3.30)
where vx and vy, are the uniform horizontal and vertical velocities.
A direct consequence of (3.30) is a differential equation which relates vx
and vy,to ![]() and
and ![]() , which is valid in the spatiotemporal
region over which uniform translational motion is assumed. To derive the
relationship, let f(x,y,t-1) be denoted by s(x,y):
, which is valid in the spatiotemporal
region over which uniform translational motion is assumed. To derive the
relationship, let f(x,y,t-1) be denoted by s(x,y):
s(x,y)=f(x,y,t-1) (3.31)
From (3.30), and(3.31)
f(x,y,t)=s(a (x,y,t), b(x,y,t)), t-1 £ t £ t0 (3.32a)
a (x,y,t)=x-vx(t-t-1) (3.32b)
b (x,y,t)=y-vy(t-t-1) (3.32c)
From
(3.32), assuming ![]() and
and
![]() , and
, and ![]() exist, we obtain
exist, we obtain
![]() (3.33a)
(3.33a)
![]() (3.33b)
(3.33b)
![]() (3.33c)
(3.33c)
From (3.33)
![]() (3.34)
(3.34)
Equation (8.34) is called a spatio-temporal constraint equation and can be generalized to incorporate other types of motion, such as zooming.
The assumption of simple translation that led to (3.29) and the additional assumption of translation with uniform velocity that led to (3.34) are highly restrictive. For example, they do not allow for object rotation, camera zoom, regions uncovered by translational object motion, or multiple objects moving with different vx and vy. However, by assuming uniform translational motion only locally and estimating the two motion parameters (dx,dy) or (vx,vy) at each pixel or at each small subimage, (3.29) and (3.34) are valid for background regions that are not affected by object motion and for regions occupied by objects which do indeed translate with a uniform velocity. Such regions occupy a significant portion of a typical sequence of image frames. In addition, if we identify the regions where motion estimates are not accurate, we can suppress motion-compensated processing in those regions. In image interpolation, for example, we can assume that vx and vy are zero.
Motion estimation methods can be classified broadly into two groups, that is, region matching methods and spatio-temporal constraint methods. Region matching methods are based on (3.29), and spatio-temporal constraint methods are based on (3.34). We first discuss region matching methods.
Region matching methods. Region matching methods involve considering a small region in an image frame and searching for the displacement which produces the “best match” among possible regions in an adjacent frame, in region matching methods, the displacement vector (dx,dy) is estimated by minimizing
![]() (3.35)
(3.35)
where R is the local spatial region used to estimate (dx,dy) and C[.,.] is a metric that indicates the amount of dissimilarity between two arguments. The integrals in (3.35) can be replaced by summation if f(x,y,t) is sampled at the spatial variables (x,y). If we estimate (dx,dy) at time t0, the region R is the local spatial region that surrounds the particular spatial position at which (dx,dy) is estimated. The size of R is dictated by several considerations. If it is chosen too large, the assumption that (dx,dy) is approximately constant over the region R may not be valid and evaluation of the error expression requires more computations. If it is chosen too small, the estimates may become very sensitive to noise. One reasonable choice based on these considerations is a 5 x 5-pixel region. There are many possible choices for the dissimilarity function C[.,.]. Two commonly used choices are the squared difference and absolute difference between the two arguments. With these choices of C[.,.], (3.35) reduces to
![]() (3.36)
(3.36)
![]() (3.37)
(3.37)
The function f(x,y,t0)-f(x-dx, y-dy,t-1) is called the displaced frame difference. In typical applications of motion-compensated processing, the system performance is not very sensitive to the specific choice of the dissimilarity function.
To the extent that (3.29) is valid, the error expression in (3.36) or (3.37) is zero at the correct (dx,dy). Minimizing the Error in (3.36) or (3.37) is a nonlinear problem. Attempts to solve this nonlinear problem have produced many variations, which can be grouped into block matching and recursive methods. We discuss block matching methods first.
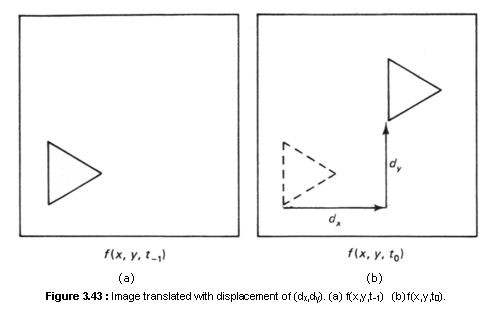
One straightforward approach to solve the above minimization problem is to evaluate the Error for every possible (dx,dy) within some reasonable range and choose (dx,dy) at which the Error is minimum. In this approach, a block of pixel intensities at time t0 is matched directly to a block at time t-1. This is the basis of block matching methods. Since the error expression has to be evaluated at many values of (dx,dy) this method of estimating (dx,dy) is computationally very expensive and many methods have been developed to reduce computations, in one simplification, we assume that (dx,dy) is constant over a block, say of 7 x 7 pixels. Under this assumption, we divide the image into many blocks and we estimate (dx,dy) for each block. Even though we generally choose the block size to be the same as the size of R in (3.35), it is not necessary to do so. In another simplification, we can limit the search space to integer values of (dx,dy) in addition to reducing the search space from continuous variables (dx,dy) to discrete variables, limiting the search space to integer values allows us to determine f(n1-dx, n2-dy), necessary in the evaluation of the error expression, without interpolation. However, the estimates of (dx,dy) are restricted to discrete values.
We can reduce the computational requirements in block matching methods further
by using a more efficient search procedure than a brute force search. One such
method is called a three-step search method, illustrated in Figure 3.44. in the
first step of this method, the error expression is evaluated at nine values of
(dx,dy) which are marked by “1’’ and filled
circles. Among these nine values, we choose (dx,dy) with
the smallest Error. Suppose the smallest Error is at (dx=3, dy=-3).
In the second step, we evaluate the error expression at eight additional values
of (dx,dy) which are marked by “2” and filled
squares. We now choose (dx,dy) from nine values
[eight new values and (dx=3, dy=-3)]. This
procedure is repeated one more time. At the end of the third step, we have an
estimate of (dx,dy). This procedure can be easily
generalized to more than three steps to increase the range of possible (dx,dy).
Another search method is to estimate dx first by searching (dx,0).
Once dx is estimated, say ![]() , dy is estimated by searching
, dy is estimated by searching
![]() . If we wish
to improve the estimate further, we can reestimate dx by
searching
. If we wish
to improve the estimate further, we can reestimate dx by
searching ![]() where
where
![]() is
the estimate of dy, obtained in the previous step. At each step in
this procedure, we estimate only one parameter, which is considerably simpler
than estimating two parameters jointly. These heuristic methods reduce the
number of computations by reducing the number of values of (dx,dy)
at which the error expression is evaluated. However, the Error at the estimated
(dx,dy) may not be the global minimum.
is
the estimate of dy, obtained in the previous step. At each step in
this procedure, we estimate only one parameter, which is considerably simpler
than estimating two parameters jointly. These heuristic methods reduce the
number of computations by reducing the number of values of (dx,dy)
at which the error expression is evaluated. However, the Error at the estimated
(dx,dy) may not be the global minimum.
In block matching methods, we estimate (dx,dy) by explicitly evaluating the Error at some specified set of (dx,dy). As an alternative, we can use descent algorithms such as the steepest descent, to solve the nonlinear problem of minimizing the Error with respect to (dx,dy). In this class of algorithms, a recursive (iterative) procedure is used to improve the estimate in each iteration. For this reason, they are called recursive in methods.
Let ![]() denote
the estimate of (dx,dy) after the k th iteration. In
recursive methods, the estimate of (dx,dy) after the k +1
th iteration,
denote
the estimate of (dx,dy) after the k th iteration. In
recursive methods, the estimate of (dx,dy) after the k +1
th iteration, ![]() is
obtained by
is
obtained by
![]() (3.38a)
(3.38a)
![]() (3.38b)
(3.38b)
where ux(k) and uy(k) are the update or correction terms. The update terms vary depending on the descent method used. If we use the steepest descent method, for example, (3.38) becomes
![]() (3.39a)
(3.39a)
![]() (3.39b)
(3.39b)
where Î is a step size that can be adjusted and Error(dx,dy) is the Error in (3.35) as a function of dx and dy for a given R. Recursive methods typically involve partial derivatives and tend to be sensitive to the presence of noise or fine details in an image. Smoothing the image before motion estimation often improves the performance of recursive methods.
In recursive methods, (dx,dy) is not limited to integer values and can be estimated within subpixel accuracy. Update terms typically include evaluation of partial derivatives of Error(dx,dy), which involves evaluation of f(x,y,t-1) and its partial derivatives at an arbitrary spatial point. In practice, f(x,y,t-1) is known only at x=n1T1 and y=n2T2. To evaluate the necessary quantities at an arbitrary spatial point (x,y), we can use the spatial interpolation techniques discussed in Section 3.4.1.
In recursive methods, (dx,dy) is typically estimated at
each pixel. In using the recursion relationship in (3.38), (dx(0),dy(0))
is typically obtained from the estimate at the adjacent pixel in the same
horizontal scan line, in the adjacent scan line, or in the adjacent frame. These
methods are called pel (picture element) recursive estimation with horizontal,
vertical, and temporal recursion. respectively. Given ![]() , we can use the recursion
relation in (3.38) only once for a pixel and then move on to the next pixel.
Alternatively, we can use the recursion relation more than once for a more
accurate estimate of (dx,dy) before we move on to the
next pixel.
, we can use the recursion
relation in (3.38) only once for a pixel and then move on to the next pixel.
Alternatively, we can use the recursion relation more than once for a more
accurate estimate of (dx,dy) before we move on to the
next pixel.
Although we classified region matching methods into block matching methods and recursive methods to be consistent with the literature, the boundary between the two classes of methods is fuzzy. By choosing a finer grid at which the error expression is evaluated, we can also estimate (dx,dy) within subpixel accuracy with block matching methods, in addition, the three-step search procedure discussed as a block matching method can be viewed as a recursive method in which the estimate is improved iteratively. A major disadvantage of region matching methods is in the amount of computation required. Even though only two parameters, dx and dy must be estimated, solving the nonlinear problem at each pixel or at each small subimage can be computationally very expensive.
Spatio-temporal constraint methods. Algorithms of this class are based
on the spatio-temporal constraint equation (3.34), which can he viewed as a
linear equation for two unknown parameters vx, and vy
under the assumption that ![]() and
and ![]() , and
, and ![]() are given. By evaluating
are given. By evaluating ![]() ,
, ![]() , and
, and ![]() at many points (xi,yi,ti)
for 1£ i £ N at which vx, and vy are
assumed constant, we can obtain an overdetermined set of linear equations:
at many points (xi,yi,ti)
for 1£ i £ N at which vx, and vy are
assumed constant, we can obtain an overdetermined set of linear equations:
![]() (3.40)
(3.40)
The velocity estimates can be obtained by minimizing
![]() (3.41)
(3.41)
Since the error expression in (3.41) is a quadratic form of the unknown parameters vx and vy, the solution requires solving two linear equations. More generally, suppose (3.34) is valid in a local spatio-temporal region denoted by ‘1’. To estimate vx and vy we minimize
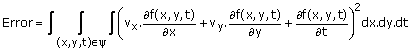 (3.42)
(3.42)
The integrals in (3.42) may be replaced by summations. One such example is (3.41). Differentiating the Error in (3.42) with respect to vx and vy and setting the results to zero leads to
Wv = g (3.43a)
where
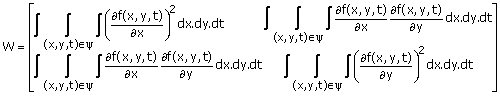 (3.43b)
(3.43b)
v = [vx,vy]T
(3.43c)
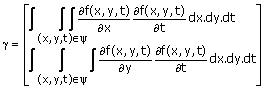
The
two linear equations in (8.43) may have multiple solutions. Suppose f(x,y,t)
is constant in the spatio-temporal region y. Then ![]() ,
, ![]() , and
, and ![]() are all zero, and all the elements in W
and g in
(3.43) are zero. Therefore, any (vx,vy) will satisfy
(3.43a). Any velocity in a unitorm intensity region will not affect f(x,y,t),
so the true velocity cannot be estimated from f(x,y,t). Suppose
f(x,y,t) is a perfect step edge. The velocity along the direction
parallel to the step edge will not affect f(x,y,t) and therefore cannot
be estimated. These problems have been studied, and a solution has been
developed. Let l1 and l2 denote the eigenvalues of W, and let a1 and a1 denote the corresponding
orthonormal eigenvectors. A reasonable solution to (3.43) is given by (see
Problem 3.24)
are all zero, and all the elements in W
and g in
(3.43) are zero. Therefore, any (vx,vy) will satisfy
(3.43a). Any velocity in a unitorm intensity region will not affect f(x,y,t),
so the true velocity cannot be estimated from f(x,y,t). Suppose
f(x,y,t) is a perfect step edge. The velocity along the direction
parallel to the step edge will not affect f(x,y,t) and therefore cannot
be estimated. These problems have been studied, and a solution has been
developed. Let l1 and l2 denote the eigenvalues of W, and let a1 and a1 denote the corresponding
orthonormal eigenvectors. A reasonable solution to (3.43) is given by (see
Problem 3.24)
Case 1. v = 0, l1, l2 < threshold (3.44a)
Case
2. ![]()
![]() >>
>>![]() (3.44b)
(3.44b)
Case 3. v = W-1 . g, otherwise (3.44c)
Case 1 includes the uniform intensity region, where the velocity is set to zero. Case 2 includes the perfect step edge region, and the velocity estimate in (3.44b) is along the direction perpendicular to the step edge.
Solving the linear equations in (3.43) requires evaluation of ![]() ,
, ![]() , and
, and ![]() at arbitrary spatio-temporal
positions. This can be accomplished by extending the spatial polynomial
interpolation method to 3-D. which has the advantage over other approaches in
computational simplicity and robustness to noise. In the 3-D polynomial
interpolation, the interpolated
at arbitrary spatio-temporal
positions. This can be accomplished by extending the spatial polynomial
interpolation method to 3-D. which has the advantage over other approaches in
computational simplicity and robustness to noise. In the 3-D polynomial
interpolation, the interpolated ![]() is
is
![]() (3.45)
(3.45)
An
example of ![]() for
N = 9 is
for
N = 9 is
![]() = 1, x, y, t, x2, y2,
xy, xt, yt. (3.46)
= 1, x, y, t, x2, y2,
xy, xt, yt. (3.46)
The coefficients Si can be determined by minimizing
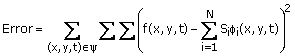 (3.47)
(3.47)
One
reasonable choice of the region y typically contains 50 pixels: 5 for n1, 5 for
n2 and 2 for t. Minimizing the error expression in (3.47)
with respect to Si requires solving a set of linear equations. Note
that the partial derivatives ![]() ,
, ![]() , and
, and ![]() used in (2.43) can be precomputed in
terms of Si.
used in (2.43) can be precomputed in
terms of Si.
The motion estimation algorithms discussed above require determination of the spatio-temporal regions denoted by y over which the uniform translational motion can be assumed. Since a local spatial region in a frame is on the order of 5 x 5 pixels in size, determining a reasonable y requires an initial displacement estimate within a few pixels of the true displacement. In practice, it is not uncommon for the displacement between two adjacent frames to be on the order of 10 pixels. One approach to obtaining an initial displacement (or velocity) is to use a previously computed velocity in the neighborhood and then determine the appropriate y as shown in Figure 3.45. Another approach is the hierarchical method or the multigrid method. The multigrid method begins with the velocity estimated on a coarse grid. The coarse grid has been obtained from the original frame by lowpass filtering and down-sampling. Down-sampling contracts the displacement (or velocity). A large velocity in the original frame is scaled down by the down-sampling factor. The velocities in the down-sampled frames can be estimated by using the spatio-temporal constraint method with an assumed initial velocity of zero. The velocities estimated on the coarse grid are interpolated to generate initial estimates of the velocities at a finer grid. The bilinear interpolation may be used in the velocity interpolation. The multigrid method can be viewed as an example of pyramid processing, which exploits a data structure called a pyramid. A pyramid provides successively condensed information of an image. An example of a pyramid is a higher resolution image and successively lower resolution images. Pyramid processing is useful in various applications including image coding and is discussed further in Chapter 5.
A major advantage of the spatio-temporal constraint methods over region matching methods is their computational simplicity, in addition, preliminary studies based on both synthetic and real data indicate that a spatio-temporal constraint method with polynomial interpolation for f(x,y,t) performs as well as a region matching method for both noisy and noise -free image frames.
Both the region matching and spatio-temporal constraint methods can produce substantial errors in motion estimation for some regions, either because the signal f(x,y,t) cannot be modeled by uniform translational motion, or because the motion estimation algorithm does not perform well, perhaps due to the presence of noise. One means of detecting large errors is to compare the error expression in (3.35) for region niatching methods or the error expression in (3.42) for spauio temporal constraint methods with some threshold. The regions where the error is above the threshold can be declared to have unreliable motion estimates, and motion-compensated processing can be suppressed in such regions.