3.3.4. Edge Detection Based on Signal Modeling
The edge detection algorithms discussed above are general methods, in that they are developed independent of an application context. An alternative approach is to develop an edge detection algorithm specific to a particular application problem. If we know the shape of an edge, for example, this information can be incorporated in the development of an edge detection algorithm. To illustrate how an edge detection algorithm specific to an application problem may be developed, we consider the problem of detecting boundaries of coronary arteries from an angiogram.
The coronary arteries are the blood vessels, which encircle the heart and supply blood to the heart muscle. Narrowing of the coronary arteries prevents adequate blood supply from reaching the heart, causing pain and damage to the heart muscle. Such damage is called coronary disease. To determine the severity of coronary disease, a coronary angiogram is used. An angiogram is an X-ray picture of arteries taken after a contrast agent, typically iodine, has been injected into the vessels. The contrast agent is injected directly into the arteries through a catheter in order to achieve high concentrations. An example of a coronary angiogram is shown in Figure 3.38. Different observers making conventional visual evaluations of an angiogram will give widely varying evaluations of the severity of the disease.
The most commonly used measure of an obstruction is percentage of stenosis, which is defined as the maximum percentage of arterial narrowing within a specified length of the vessel. One approach to estimating the percentage of stenosis begins with determining the vessel boundaries from an angiogram. We will be concerned with the problem of detecting the vessel boundaries.
One reasonable model of an angiogram f(n1,n2) is given by
f(n1,n2)= (v(n1,n2)+ p(n1,n2)) * g(n1,n2)+w(n1,n2) (3.20)
where v(n1,n2) denotes the vessel, p(n1,n2) denotes the background, g(n1,n2) denotes blurring, and w(n1,n2) denotes the background noise. The vessel function v(n1,n2) is derived from a generalized cone model of a 3-D vessel which is continuous and has elliptical cross sections. The elliptical shape is chosen because of the small number of parameters involved in its characterization and because of some empirical evidence that it leads to a good estimate of percentage of stenosis. The 1-D cross section of v(n1,n2), which consists of one blood vessel, is totally specified by three parameters, two representing the blood vessel boundaries and one related to the x-ray attenuation coefficient of iodine. The continuity of the vessel is guaranteed by fitting a cubic spline function to the vessel boundaries. The background p(n1,n2) is modeled by a 2-D low-order polynomial. Low-order polynomials are very smooth functions, and their choice is motivated by the observation that objects in the background, such as tissue and bone, are much bigger than the blood vessels. The blurring function g(n1,n2) is modeled by a known 2-D Gaussian function that takes into account the blurring introduced at various stages of the imaging process. The noise w(n1,n2) is random background noise and assumed to be white. The parameters in the model of f(n1,n2) are the vessel parameters, the polynomial coefficients of p(n1,n2), and the noise variance.
The vessels, tissues, bones, and the radiographic imaging process are much more
complicated than suggested by the simple model presented above. Nevertheless,
the model has been empirically observed to lead to good estimates of the vessel
boundaries and corresponding percentage of stenosis. The model parameters may
be estimated by a variety of different procedures. One possibility is the
maximum likelihood (ML) parameter estimation method. In the ML method, the
unknown parameters denoted by 0 are estimated by maximizing the probability
density function ![]() where
f(n1,n2) is the angiogram observation and 0 represents
all the unknown parameters to be estimated. The ML method applied to vessel
boundary detection is a nonlinear problem, but has been solved approximately.
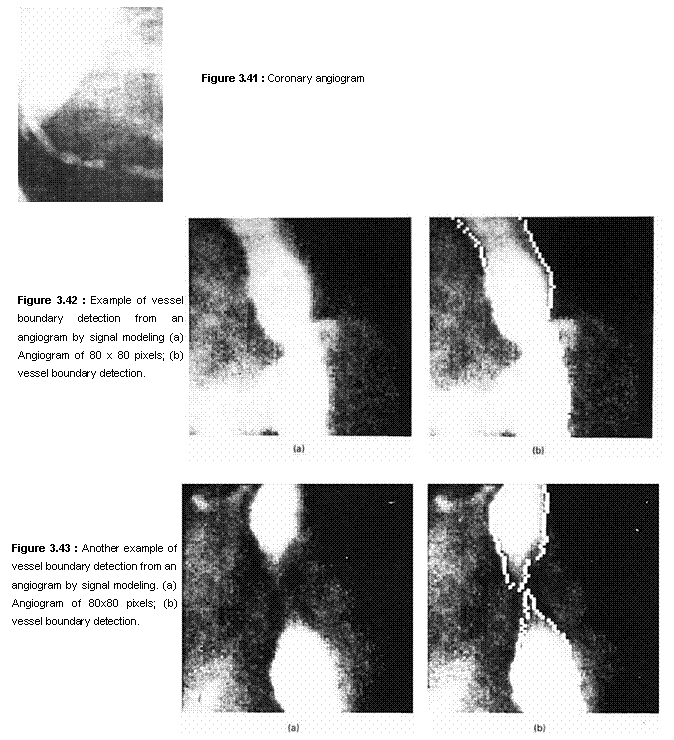
Figures 3.42 and 3.43 illustrate the results of applying the ML parameter
estimation method to the detection of the blood vessels using the 1-D version
of the 2-D model in (3.20). In the 1-D version, f(n1,n2) in
(3.20) is considered a 1-D sequence with variable n1 for each n2.
Computations simplify considerably when the 1-D model is used. Figure 3.42(a)
shows the original angiogram of 80 x 80 pixels, and Figure 3.42(b) shows the
detected vessel boundaries superimposed on the original image. Figure 3.43 is
another example. Developing an edge detection algorithm specific to an
application problem is considerably more complicated than applying the general
edge detection algorithms discussed in previous sections. However, it has the
potential of leading to much more accurate edge detection.
where
f(n1,n2) is the angiogram observation and 0 represents
all the unknown parameters to be estimated. The ML method applied to vessel
boundary detection is a nonlinear problem, but has been solved approximately.
Figures 3.42 and 3.43 illustrate the results of applying the ML parameter
estimation method to the detection of the blood vessels using the 1-D version
of the 2-D model in (3.20). In the 1-D version, f(n1,n2) in
(3.20) is considered a 1-D sequence with variable n1 for each n2.
Computations simplify considerably when the 1-D model is used. Figure 3.42(a)
shows the original angiogram of 80 x 80 pixels, and Figure 3.42(b) shows the
detected vessel boundaries superimposed on the original image. Figure 3.43 is
another example. Developing an edge detection algorithm specific to an
application problem is considerably more complicated than applying the general
edge detection algorithms discussed in previous sections. However, it has the
potential of leading to much more accurate edge detection.