3.1.3. Homomorphic Processing
When an image with a large dynamic range, for instance, a natural scene on a sunny day, is recorded on a medium with a small dynamic range, such as film or paper, the image’s contrast is significantly reduced, particularly in the dark and bright regions. One approach to enhancing the image is to reduce its dynamic range and increase its local contrast prior to recording it on a medium with a small dynamic range.
One method developed to reduce the dynamic range and increase the local contrast is based on applying a homomorphic system for multiplication to an image formation model. An image is typically formed by recording the light reflected from an object that has been illuminated by some light source. Based on this observation, one simple model of an image is
f(n1,n2)= i(n1,n2).r(n1,n2) (3.4)
where i(n1,n2) represents the illumination and r(n1,n2) represents the reflectance. In developing a homomorphic system for image enhancement, the illumination component i(n1,n2) is assumed to be the primary contributor to the dynamic range of an image and is assumed to vary slowly, while the reflectance component r(n1,n2) that represents the details of an object is assumed to be the primary contributor to local contrast and is assumed to vary rapidly. To reduce the dynamic range and increase the local contrast, then, we need to reduce i(n1,n2) and increase r(n1,n2). To separate i(n1,n2) from r(n1,n2) in (3.4), a logarithmic operation is applied to (3.4) and the result is
log f(n1,n2)= log i(n1,n2) + log r(n1,n2). (3.5)
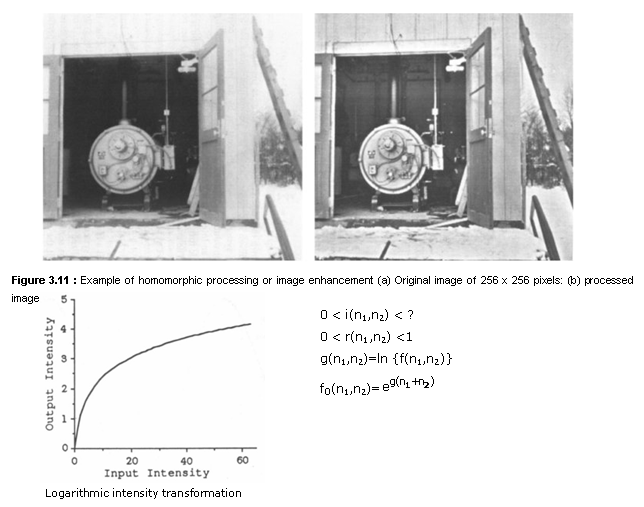
If we assume that log i(n1,n2) remains slowly varying and log r(n1,n2) remains rapidly varying, lowpass filtering log f(n1,n2) will result in log i(n1,n2) and highpass filtering log f(n1,n2) will result in log r(n1,n2). Once log i(n1,n2) and log r(n1,n2) have been separated at least approximately, log i(n1,n2) is attenuated to reduce the dynamic range while log r(n1,n2) is emphasized to increase the local contrast. The processed log i(n1,n2) and log r(n1,n2) are then combined and the result is exponentiated to, get back to the image intensity domain. This is shown in Figure 3.10(a). The system in Figure 3.10(a) can be simplified by replacing the system inside the dotted line in the figure with the corresponding highpass filter. The simplified system is shown in Figure 3.10(b). An example illustrating the performance of the system in Figure 3.10(b) is shown in Figure 3.11. Figure 3.11(a) shows an original image of 256 x 256 pixels and Figure 3.11(b) shows the processed image using the system in Figure 3.10(b).
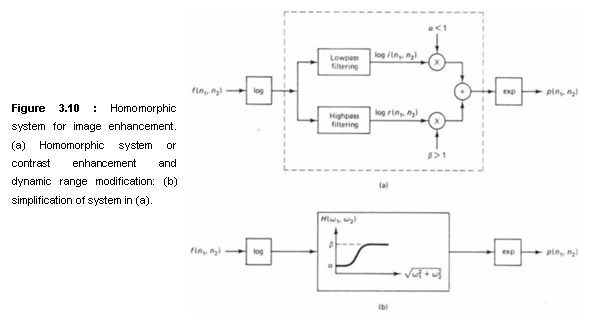
A system like that in Figure 3.10, which performs a logarithmic operation followed by a linear operation followed by an exponentiation operation, is called a homomorphic system for multiplication. This is the origin of the terms homomorphic processing and homomorphic filtering. The logarithmic operation transforms multiplicative components to additive components. The linear operation performs the separation by exploiting characteristics of the resulting additive components and processes the separated components. The exponentiation operation brings the processed signal back to the original signal domain.
Although the system in Figure 3.10 was developed from a model of image formation and a homomorphic system, the system can be viewed simply as highpass filtering in the log intensity domain. Performing highpass filtering in the log intensity domain is also reasonable in light of human visual system. The image intensity appears to be modified at the peripheral level of a human visual system by some form of nonlinearity such as a logarithmic operation. Thus, the log intensity domain is, in a sense, more central to the human visual system than is the intensity domain.