3.1. CONTRAST AND DYNAMIC RANGE MODIFICATION
3.1.1. Gray Scale Modification
Gray scale modification is a simple and effective way of modifying an image’s dynamic range (the range of image intensities) or contrast. In this method, the gray scale or intensity level of an input image f(n1,n2) is modified according to a specific transformation. The transformation g=T[f] that relates an input intensity f to an output intensity g is often represented by a plot or a table. Consider a simple illustration of this method. Figure 3.1(a) shows an image of 4 x 4 pixels, with each pixel represented by three bits, so that there are eight levels; that is, f = 0 (darkest level), 1, 2,………..,7 (brightest level). The transformation that relates the input intensity to the output intensity is shown as a plot and as a table in Figure 3.1(b). For each pixel in the input image, the corresponding output intensity is obtained from the plot or the table in Figure 3.1(b). The result is shown in Figure 3.1(c). By properly choosing the specific transformation, contrast or dynamic range can be modified.

The specific transformation desired depends on the application. In sonic applications, physical considerations determine the transformation selected. For example, when a display system has nonlinear characteristics, the objective of the modification may be to compensate for the nonlinearities. In such a case, the most suitable transformation can be determineo from the nonlinearity of the display system.
A good transformation in typical applications can be identified by computing the histogram of the input image and studying its characteristics. The histogram of an image, denoted by p(f), represents the number of pixels that have a specific intensity f as a function of f. For example, the 4 x 4-pixel image shown in Figure 3.1(a) has the histogram shown in Figure 3.2(a). The histogram displays some important image features that help determine which particular gray scale transformation is desirable, in Figure 3.2(a), the image’s intensities are clustered in a small region, and the available dynamic range is not very well utilized. In such a case, a transformation of the type shown in Figure 3.1(b) would increase the overall dynamic range, and the resulting image would appear to have greater contrast. This is evidenced by Figure 3.2(b), which is the histogram of the processed image shown in Figure 3.1(c).

Because computing the histogram of an image and modifying its gray scale for a given gray scale transformation requires little computation, the desirable gray scale transformation can be determined by an experienced human operator in real-time. On the basis of the initial histogram computation, the operator chooses a gray scale transformation to produde a processed image. By looking at the processed image and its histogram, the operator can choose another gray scale transformation, obtaining a new processed image. These steps can be repeated until the output image satisfies the operator.
In such circumstances as when there are too many images for individual attention by a human operator, the gray scale transformation must be chosen automatically. A method known as histogram modification is useful in this case. In this method, the gray scale transformation that produces a desired histogram is chosen for each individual image. The desired histogram of the output image, denoted by pd(g), that is useful for typical images has a maximum around the middle of the dynamic range and decreases slowly as the intensity increases or decreases. For a given image, we wish to determine the transformation function so that the resulting output image has a histogram similar to pd(g). This problem can be phrased in terms of a problem in elementary probability theory. Specifically, the histograms p(f) and pd(g) can he viewed as scaled probability density functions of random variables f and g, respectively. For example, p(3)/16 in Figure 3.2(a)is the probability that a randomly chosen pixel in the 4x4-pixel image in Figure 3.1(a) will have an intensity level of 3. We wish to find a transformation g=T[f] with the constraint that T[f] must be a monotonically nondecreasing function of f such that p(g) is equal to or close to pd(g). One approach to solving this probability problem is to obtain the probability distribution functions P(f) and Pd(g) by integrating the probability density functions p(f) and pd(g) and then choosing the transformation function such that P(f) will be equal to or close to Pd(g) at g=T[f]. Imposing the constraint that T[f] must be a monotonicallv nondecreasing function ensures that a pixel with a higher intensity than another pixel will not become a pixel with a lower intensity in the output image.
Applying this approach to the histogram modification problem which involves discrete variables f and g, we first compute the cumulative histograms P(f) and Pd(g) from p(f) and pd(g) by
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
An example of the cumulative histograms is shown in Figure 3.3. Figures 3.3(a and (b) show an example of p(f) and pd(g) and Figures 3.3(c) and (d) show P(f) and Pd(g) obtained by using (3.1). From P(f) and Pd(g), the gray scale transformation g = T[f] can be obtained by choosing g for each f such that Pd(g) will be closest to P(f). The gray scale transformation function obtained from Figure 3.3 is shown in Figure 3.4(a). and the histogram of the image obtained by using this transformation function is shown in Figure 3.4(b). If the desired histogram pd(g) remains the same for different input images, Pd(g) needs to be computed only once from pd(g).
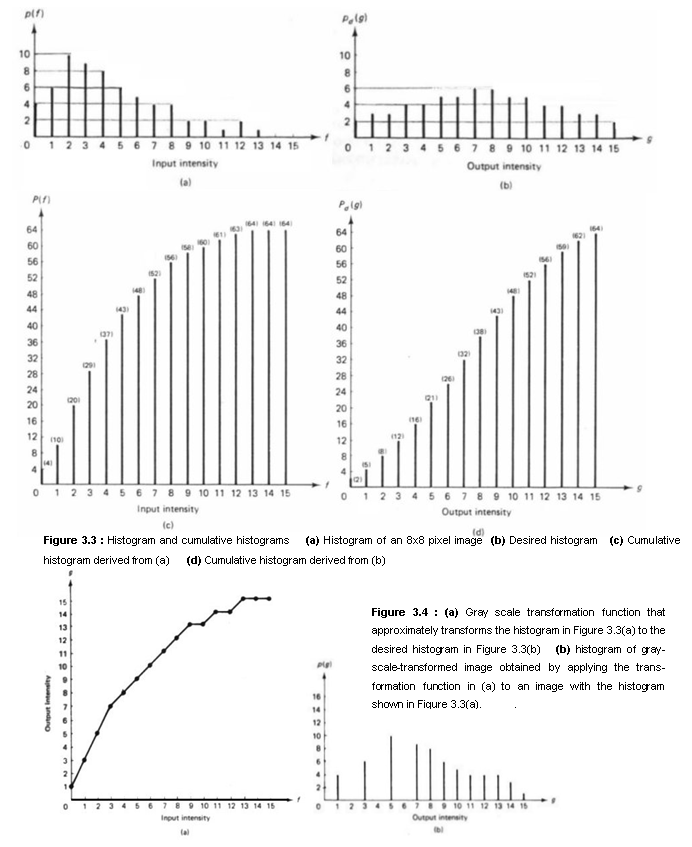
In the example we considered above, note that the histogram of the processed image is not the same as the given desired histogram. This is in general the case when f and g are discrete variables and we require that all the pixels with the same input intensity be mapped to the same output intensity. Note also that the desired cumulative histogram Pd(g) is close to a straight line. In the special case of the histogram modification known as histogram equalization, the desired histogram is assumed constant. In this case, the desired cumulative histogram would be exactly a straight line. Image processed by histogram equalization typically have more contrast than unprocessed images, but they tend to appear somewhat unnatural.
Even though gray scale modification is conceptually and computationaly simple, it can provide significant improvement in image quality or intelligibility to the human observer, and therefore used routinely in many image processing applications. This is illustrated in the following two examples. Figure 3.5(a) shows an original image of 512 x 512 pixels. with each pixel represented by eight bits. Figure 3.5(h) shows the histogram of the image in Figure 3.5(a). The histogram clearly shows that a large number of the image~s pixels are concentrated in the lower intensity levels of the dynamic range. suggesting that the image will appear very dark with a loss of contrast in the dark regions. By increasing the contrast in the dark regions. the details can be made more visible. This can be accomplished by using the transformation function shown in Figure 3.5(c). The processed image using the function in Figure 3.5(c) is shown in Figure 3.5(d), and the histogram of the processed image is shown in Figure 3.5(e). Another example is shown in Figure 3.6. The unprocessed image is shown in Figure 3.6(a) and the image processed by gray scale modification is shown in Figure 3.6(b).
The histogram modification method discussed above can also be applied to color images. To improve the image contrast with only a relatively small effect on the hue or saturation, we can transform RGB images fR(n1,n2), fG(n1,n2), and fB(n1,n2) to YIQ images fY(n1,n2), fI(n1,n2), and fQ(n1,n2) by using the transformation
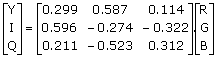 .
.
Gray scale modification can be applied to only the Y image fY(n1,n2), and the result can be combined with the unprocessed fI(n1,n2) and fQ(n1,n2). Again using the transformation

the processed RGB images gR(n1,n2), gG(n1,n2), and gB(n1,n2) can be obtained. Figure 3.7(a) shows an original color image of 512 x 512 pixels. and Figure 3.7(b) shows the image processed by the gray scale transformation discussed above.

