2.3. VISUAL PHENOMENA 

2.3.1. Intensity Sensitivity

One way to quantify our ability to resolve two visual stimuli which are the same except for their intensities or luminances is by measuring the just-noticeable difference (j.n.d.). The j.n.d. can be defined and measured in a variety of ways. One way is through a psychophysical experiment called intensity discrimination. Suppose we present the visual stimulus in Figure 2.16 to an observer. The inside region is a monochrome image of uniform intensity I_in, which is randomly chosen to be either I or I + DI. The outside region is a monochrome image of intensity I_out, which is chosen to be I + DI when I_in =I and I when I_in = I + DI. The observer is asked to make a forced choice as to which of the two intensities I_in, and I_out is brighter. When DI is very large, the observer will give a correct answei most of the time, correct in the sense that the region with I+DI is chosen. When DI is very small, the observer will give a correct answer about half of the time. As we move away from a very large DI to a very small DI, the percentage of the observer’s correct responses decreases continuously, and we can define DI at which the observer gives correct responses 75% of the time as the j.n.d. at the intensity I.

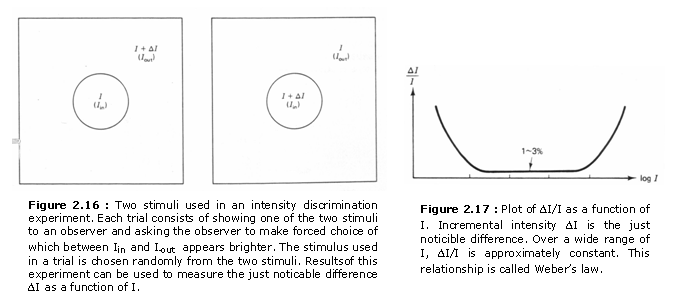
The result of plotting DI/I as a function of I where DI is the j.n.d. is shown in Figure 2.17. From the figure, for a wide range of I,

. (2.9)

This relationship is called Weber’s law. Weber’s law states that the j.n.d. DI is proportional to I. As we increase I, we need a larger DI to make I + DI noticeably different from I. This is one way in which the visual system remains sensitive to a wide dynamic range of the visual stimulus intensity. Weber’s law holds approximately not only for vision, but also for all other human sense modalities: hearing, smell, taste, and touch.

As we let DI approach 0, (2.9) can be written as

(2.10)

From (2.10), the j.n.d. is constant in the log I domain for a wide range of I. This is consistent with the notion that a nonlinear operation such as the log is applied to the image intensity in the simple model in Figure 2.15. The intensity discrimination experiment involves a very simple task on the part of the observer, and complicated central level processing probably is not needed. Consequently, the result of the intensity discrimination experiment can be related to peripheral level processing in the visual system.

The result of the intensity discrimination experiment states that the j.n.d. DI increases as I increases. This partly explains why a uniform level of random noise is more visible in a darker region than in a brighter region. This is illustrated in Figure 2.18. The image in Figure 2.18 is the result of adding zero-mean white noise with a uniform probability density to an original undegraded image. The grainy appearance, which is due to noise, is more pronounced in the darker uniform background region than in the brighter uniform background region. Since the j.n.d. DI is larger for a larger I, a higher level of noise in the brighter region is required for it to he equally visible as a lower level of noise in the darker region. The implication of this observation for image processing is that reducing noise in the darker region is more important than reducing noise in the brighter region.