2.1.2. Brightness, Hue, and Saturation

Human perception of light with c(λ) is generally described in terms of brightness, hue, and saturation.

· Brightness refers to how bright the light is.

· Hue refers to the color, such as red, orange, or purple.

· Saturation, sometimes called chroma, refers to how vivid or dull the color is.

Brightness, hue, and saturation are perceptual terms, and they depend on a number of factors, including the detailed shape of c(λ).But, it is possible to relate them very approximately to specific features of c(λ).

To relate the human perception of brightness to c(λ), it is useful to define photometric quantities. The quantities associated with c(λ), such as radiant flux, irradiance, and watts/m², are called radiometric units. These physical quantities can be defined independent of a specific observer. The contributions that c(λ₁) and c(λ₂) make to human perception of brightness are in general quite different for λ₁ ≠ λ₂  even though c(λ₁)may be the same as c(λ₂). For example, an electromagnetic wave with c(λ) is invisible to a human observer as long as c(λ) is zero in the visible range of λ, no matter how large c(λ) may be outside the visible range. Even within the visible range. the brightness depends on λ. For this reason, a simple integral of c(λ) over the variable λ does not relate well to the perception of brightness. The quantities which take the human observer’s characteristics into account, thus relating to brightness better than the integral of c(λ) are called photometric quantities.

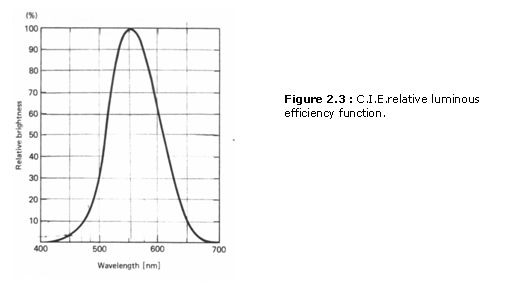
The basic photometric quantity is luminance, adopted in 1948 by the C.I.E. (Commission lnternationale de l’Eclairage), an international body concerned with standards for light and color. Consider a light with c(λ) that is zero everywhere except at λ = λ_r, where λ_r denotes a fixed reference wavelength. A light that consists of only one spectral component (one wavelength) is called a monochromatic light. Suppose we ask a human observer to compare the brightness from a monochromatic light with c(λ_r) with that from another monochromatic light with c’(λ_t) where λ_t, is a test wavelength. Suppose further that the observer says that c(λ_r) matches c(λ_t) in brightness. The equal brightness points c(λ_r) and c’(λ_t) can be obtained by such experiments as showing two patches of light with a fixed c(λ_r) and a variable c’(λ_t) and asking the observer to decrease or increase the amplitude of c’(λ_t) until they match in brightness. The ratio c(λ_r)/c’(λ_t) where c(λ_r) and c’(λ_t) match in brightness, is called the relative luminous efficiency of a monochromatic light with λ_t relative to λ_r and is approximately independent of the amplitude of c(λ_r) under normal viewing conditions. The wavelength λ_r used is 555 nm (yellowgreen light), at which a typical observer has maximum brightness sensitivity. For this choice of λ_r the relative luminous efficiency c(λ_r)/c’(λ_t) is always less than or equal to 1, since c(λ_r) is not greater than c’(λ_t); that is, it takes less energy at λ_r, to produce the same brightness. The relative luminous efficiency as a function of λ is called the relative luminous efficiency function and is denoted by v(λ). Two monochromatic lights with c₁(λ₁) and c₂(λ₂) appear equally bright to an observer when

            c₁(λ₁)v(λ₁) = c₂(λ₂)v(λ₂)                                                                  (2.5)

The relative luminous efficiency function v(λ) depends on the observer. Even with a single observer, a slightly different v(λ) is obtained when measured at different times. To eliminate this variation, the C.I.E. standard observer was defined in 1929, based on experimental results obtained from a number of different observers. The resulting function v(λ) is called the C.I.E. relative luminous efficiency function and is shown in Figure 2.3. The C.I.E. function is roughly bell-shaped with a maximum of 1 at λ = 555 nm.

The basic unit of luminance is the lumen (lm). The luminance per area 1 of a light with c(λ) can be defined by

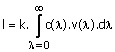                                                                               (2.6)

    In (2.6) the quantity l is in units of lumens/m², k is 685 lumens/watt, c(λ) is in units of watts/m³, v(λ) is unitless, and λ has a unit of meter. A monochromatic light with an irradiance of 1 watt/m² produces 685 lumens/m² when v(λ) = 1. This occurs when λ = 555 nm. At other wavelengths. v(λ)<1, so the irradiance of the monochromatic light must be greater than 1 watt/m to generate a luminance per area of 685 lumens/m². 

    It is important to note that the luminance or luminance per area does not measure human perception of brightness. For example, a light with 2 lumens/m² does not appear twice as bright to a human observer as a light with 1 lumen/m². It is also possible to create an environment where a light with a smaller luminance per area looks brighter than a light with a larger luminance per area. However, luminance per area is related more directly than an integral of c(λ) to human perception of brightness. Furthermore, in typical viewing conditions (light neither too weak nor excessive), a light with larger luminance per area is perceived to be brighter than a light with smaller luminance per area.

Hue is defined as that attribute of color which allows us to distinguish red from blue. In some cases, the hue of a color can be related to simple features of c(λ). Light with approximately constant c(λ) in the visible range appears white or colorless. Under normal viewing conditions, a monochromatic light appears colored and its color depends on λ. 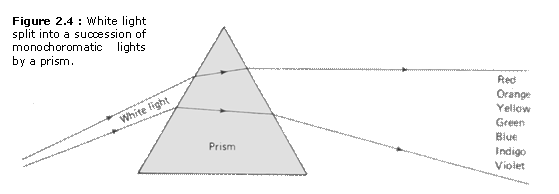When an observer is shown a succession of monochromatic lights side by side, the color changes smoothly from one hue to another. Light can be split into a succession of monochromatic lights by a prism as shown in Figure 2.4. This was first done in 1666 by Newton. Newton divided the color spectrum in the visible range into seven broad categories: red, orange. yellow, green. blue, indigo, and violet, in the order of longer to shorter λ. These are known as the seven colors of the rainbow. Newton originally began with only red, yellow, green. blue and violet. He later added orange and indigo to bring the number to seven (in keeping with the tradition of dividing the week into seven days, the musical notes into seven, and so on).

    When a light is not monochromatic but its c(λ) is narrow band in the sense that most of its energy is concentrated in  λ’-∆λ < λ < λ‘+∆λ  for small ∆λ, the perceived hue roughly corresponds to monochromatic light with λ = λ’. The color will appear less pure, however, than a monochromatic light of a similar hue. When c(λ) is some arbitrary function, it is difficult to relate the hue to some simple features of c(λ). By proper choice of c(λ), it is possible to produce hues that do not correspond to any monochromatic light. By mixing red and blue lights, for example, it is possible to produce purple light.

Saturation refers to the purity or vividness of the color. A monochromatic light has very pure spectral contents, and looks very vivid and pure. It is said to he highly saturated. As the spectral content of c(λ) widens, the color is perceived as less vivid and pure. and the color is said to be less saturated. Color saturation is related very approximately to the effective width of c(λ).