2.1. LIGHT
2.1.1. Light as an Electromagnetic Wave
Everything that we view is seen with light. There are two types of light sources.
1. Primary light source, emits its own light. Examples of primary light sources include the sun, lamps, and candles.
2. Secondary light source, only reflects or diffuses the light emitted by another source. Examples of secondary light sources include the moon, clouds, and apples.
Light is part of a vast, continuous spectrum of electromagnetic radiation. An electromagnetic wave carries energy and the energy distribution of the wave passing through a spatial plane can be represented by c(x, y, t, λ), where x and y are two spatial variables, t is the time variable, and λ is the wavelength. The function c(x, y, t, λ) is called radiant flux per (area X wavelength) or irradiance per wavelength.
 (2.1)
(2.1)
The wavelength λ is related to the frequency f by;
![]() (2.2a)
(2.2a)
where c is the speed of an electromagnetic wave, approximately 3 x 108 m/sec in vacuum and air.
![]() (2.2b)
(2.2b)
Although the function c(x, y, t, λ) can be expressed in terms of the frequency f, it is more convenient to use the wavelength λ. The unit associated with c(x, y, t, λ) is energy per (area X time X wavelength) and is joules/ (m3 sec) in the MKS (meter, kg, second) system.
![]() (2.3)
(2.3)
If we integrate c(x, y, t, λ) with respect to λ, we obtain irradiance that has the unit of joules/(m2 sec) or watts/m2.
![]() (2.4a)
(2.4a)
![]() (2.4b)
(2.4b)
![]()
Radiation from the sun that passes through a spatial plane perpendicular to the rays has 1350 watts/m2 of irradiance in the absence of atmospheric absorption. If we integrate c(x, y, t, λ) with respect to all four variables x, y, t, and λ, we obtain the total energy (in joules) of the electromagnetic wave that passes through the spatial plane.
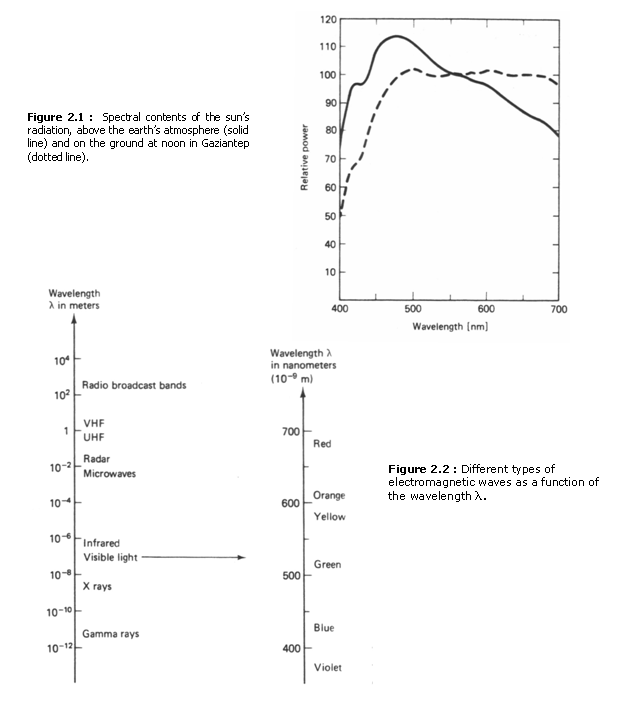
Light is distinguished from other electromagnetic waves—for instance, radio transmission waves—by the fact that the eye is sensitive to it. Suppose we consider a fixed spatial point (x’, y’) and a fixed time t’. The function c(x, y, t, λ) can be viewed as a function of λ only. We can express it as c(x’, y’, t’, λ) or c(λ) for convenience. An example of c(λ) for the radiation from the sun is shown in Figure 2.1. The eye is sensitive to electromagnetic waves over an extremely narrow range of λ, that is, approximately from 350 nm to 750 nm. (1 nm = 10-9 meter).
Figure 2.2 shows different types of electromagnetic waves as a function of the wavelength λ. Electromagnetic
radiation with large λ from a few centimeters to several thousand meters can be generated by electrical circuits. Such radiation is used for radio transmission and radar. Radiation with λ just above the visible range is called infrared; with λ just below the visible range, it is called ultraviolet. Both infrared and ultraviolet radiations are emitted by typical light sources such as the sun. Radiation with λ far below the visible range includes X rays, y rays, and cosmic rays; for cosmic rays, λ is less than 10-5 nm or 10-14 m.