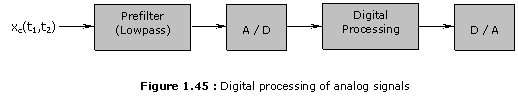1.5  DIGITAL PROCESSING OF ANALOG SIGNALS

 

    Most signals that occur in practice are analog. Since the issues that arise in digital processing of analog signals are essentially the same in both the 1-D and 2-D cases. Let’s  briefly summarize the 2-D results.

    Consider an analog 2-D signal xc(t1,t2). We’ll denote its analog Fourier transform by Xc(W1,W2). Suppose we obtain a discrete-space signal x(n3. n2) by sampling the analog signal x(n1,n2) wth sampling period (T1, T2) as follows:

                                                                           (1.56)

 

Equation (1.56) represents the input-output relationship of an ideal analog-to-digital (A/D) converter. The relationship between , the discrete-space Fourier transform of x(n1,n2), and Xc(W1,W2), the continuous-space Fourier trans­form of xc(t1,t2) is given by

 

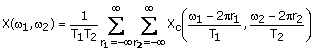                                                    (1.57)

 

Two examples of Xc(W1,W2) and  are shown in Figure 1.40. Figure 1.40(a) shows a case in which 1/T1 > W’c/ p   and  1/T2 > W’’c/ p where W’c and W’’c are the cutoff frequencies of Xc(W1,W2), as shown in the figure. Figure 1.44(b) shows a case in which 1/T1 < W’c/ p   and  1/T2 < W’’c/ p.  From the figure, when 1/T1 > W’c/ p   and  1/T2 > W’’c/ p, xc(t1,t2) can be recovered from x(n1,n2). Otherwise, xc(t1,t2) cannot be exactly recovered from x(n1,n2) without additional information on xc(t1,t2). This is the 2-D sampling theorem, and is a straightforward extension of the 1-D result.

An ideal digital-to-analog (D/A) converter recovers xc(t1,t2) from x(n1,n2) when the sampling frequencies 1/T1 and 1/T2 are high enough to satisfy the requirements of the sampling theorem. The output of the ideal D/A converter, yc(t1,t2), is given by

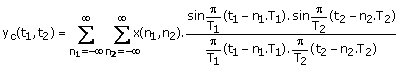                              (1.58)

 

The function yc(t1,t2) is identical to xc(t1,t2) when the sampling frequencies used in the ideal A/D converter are sufficiently high. Otherwise, yc(t1,t2) is an aliased version of xc(t1,t2). Equation (1.58) is a straightforward extension of the 1-D result.

An analog signal can often be processed by digital processing techniques using the A/D and D/A converters discussed above. The digital processing of analo1 signals can. in general. he represented by the system in Figure 1.45. The analol lowpass filter limits the bandwidth of the analog signal to reduce the effect o aliasing. In digital image processing, the analog prefiltering operation is often performed by a lens and the scanning aperture used in converting an optical image to an electrical signal. The importance of the antialiasing filter is illustrated in Figure 1.46. Figure 1.46(a) shows an image of 128 x 128 pixels with little aliasing due to an effective antialiasing filter used. Figure 1.46(b) shows an image of 128 x 128 pixels with noticeable aliasing.

(a)
 
    The A/D converter of (1.56) is based on sampling on the Cartesian grid. Th analog signal can also be sampled on a different type of grid.