1.4.3        The Projection-Slice Theorem

 

    Another property of the Fourier transform is the projection-slice theorem, which is the mathematical basis of computed tomography (CT). Computed tomography has a number of applications, including the medical application of reconstructing cross sections of a human body from x-ray images. The impact of computed tomography on medicine requires no elaboration.

Consider a 2-D analog function fc(t1,t2) where t1 and t2 are continuous var­iables. The subscript c denotes that the signal is a function of a continuous variable or variables. The analog Fourier transform Fc(W1,W2) is related to fc(t1,t2)  by

 

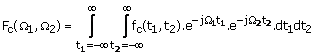                                                               (1.49 a)

 

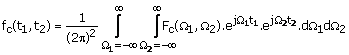                       (1.49 b)

 

 

 

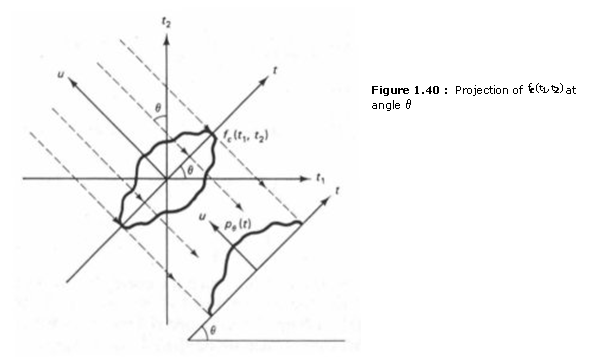
Let us integrate  along the parallel rays shown in Figure 1.40. The angle that the rays make

with the t2-axis is denoted by q. The result of the integration at a given q is a 1-D function, and we denote it by pq(t). In this figure, pq(t) is the result of integrating fc(t1,t2) along the ray passing through the origin. The function p6(t), which is called the projection of fc(t1,t2) at angle q or Radon transform of fc(t1,t2), can be expressed in terms of fc(t1,t2) by

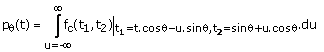                                     (1.50)

 

Equation (1.50) arises naturally from the analysis of an x-ray image. Consider a 2-D object (a slice of a 3-D object, for example) through which we radiate a monoenergetic x-ray beam, as shown in Figure 1.40. On the basis of the Lambert­Beer law, which describes the attenuation of the x-ray beam as it passes through an object, and of a model of a typical film used to record the output x-ray beam, the image recorded on film can be modeled by pq(t) in (1.50). where  is the attenuation coefficient of the 2-D object as a function of two spatial variables t1 and t2. The function  depends on the material that composes the 2-D object at the spatial position . To the extent that the attenuation coefficients of different types of material such as human tissue and bone differ, can be used to determine the types of material. Reconstructing  from the recorded pq(t) is, therefore, of considerable interest.

Consider the 1-D analog Fourier transform of pq(t) with respect to the variable and denote it by  so that

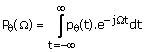                                                                           (1.51)

 

It can be shown that there is a simple relationship between  and , given by

 

                             (1.52)

 

 

 

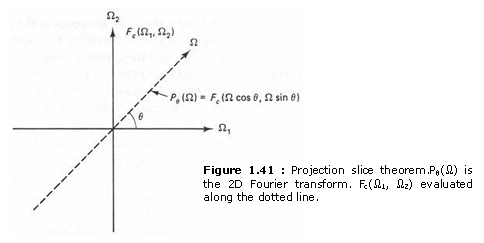
Expressed graphically, (1.52) states that the 1-D Fourier transform of the projection pq(t) is Fc(W1,W2) evaluated along the slice that passes through the origin and makes an angle of q with the W1 axis, as shown in Figure 1.41. The relationship in (1.52) is called the projection-slice theorem.

The projection-slice theorem of (1.52) can be used in developing methods to reconstruct the 2-D function fc(t1,t2) from its projections pq(t). One method is to compute the inverse Fourier transform of Fc(W1,W2) obtained from pq(t). Spe­cifically, if we compute the 1-D Fourier transform of pq(t) with respect to t for all 0 £ q < p, we will have complete information on Fc(W1,W2). In practice. of course, pq(t) cannot be measured for all possible angles 0 £ q < p, so Fc(W1,W2) must be estimated by interpolating known slices of Fc(W1,W2).

Another reconstruction method, known as the filtered back-projection method, is more popular in practice and can be derived from (1 .49b) and (1.52). It can be shown that

 

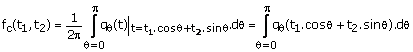              (1.53)

 

where is related to pq(t) by

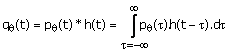                                                             (1.54)

 

The function , which can be viewed as the impulse response of a filter, is given by

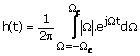                                                                                    (1.55)

 

where  is the frequency above which the energy in any projection pq(t)  can he assumed to be zero. From (1.53) and (1.54), we can see that one method of reconstructing fc(t1,t2) from pq(t) is to first compute qq(t) by filtering (convolving) pq(t) with h(t) and then to determine fc(t1,t2) from qq(t) by using (1.53). The process of determining fc(t1,t2) from qq(t) using (1.53) can be viewed as a back-projection. Consider a particular q and t, say q’ and t’. From (1.53), the values of (t1,t2) for which fc(t1,t2)  is affected by qq(t’) are given by t’ = t1.cosq’+t2.sinq’. These values are shown by the straight line in Figure  1.42. Furthermore, the contribution that qq’(t’) makes to fc(t1,t2)  is equal at all points along this line. in essence, qq’(t’) is back-projected in the (t1,t2)  domain. This back-projection takes place for all values of t’ and is integrated over all values of q’. Since qq(t) is a filtered version of pq(t), this technique is called the filtered back-projection method. In practice, pq(t) is not available for all values of q. As a result, qq(t) must be interpolated from the known slices of qq(t).

    In addition to the interpolation involved in both the direct Fourier transform method and the filtered back-projection method, a number of practical issues arise in reconstructing fc(t1,t2) from pq(t). For example, the Fourier transform, inverse Fourier transform, filtering, and integration require a discretization of the problem, which raises a variety of important issues, including sampling and aliasing. In practice, the measured function pq(t) may be only an approximate projection of fc(t1,t2). In addition, the measured data may not have been obtained from parallel-beam projection, but instead from fan-beam projection, in which case a different set of equations governs.