1.4 ADDITIONAL PROPERTIES OF THE FOURIER TRANSFORM
1.4.1 Signal Synthesis and Reconstruction from Phase or Magnitude
The Fourier transform of a sequence is in general complex-valued, and the unique representation of a sequence in the Fourier transform domain requires both the phase and magnitude of the Fourier transform. It is often desirable to synthesize or reconstruct a signal from only partial Fourier domain information.
The Fourier transform of h(n1,
n2) is said to converge to ![]() in the mean square sense when
in the mean square sense when
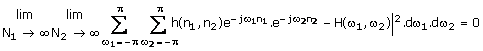
Consider a 2-D sequence x(n1,n2)
with Fourier transform ![]() so that
so that
![]() (1.42)
(1.42)
It has been observed that a straightforward signal
synthesis from the Fourier transform phase ![]() alone often
captures most of the intelligibility of the original signal x(n1,n2).
A straightforward synthesis from the Fourier transform magnitude
alone often
captures most of the intelligibility of the original signal x(n1,n2).
A straightforward synthesis from the Fourier transform magnitude ![]() alone,
however, does not generally capture the original signal’s intelligibility. To
illustrate this, we synthesize the phase-only signal xP(n1,n2)
and the magnitude-only signal xm(n1,n2) by
alone,
however, does not generally capture the original signal’s intelligibility. To
illustrate this, we synthesize the phase-only signal xP(n1,n2)
and the magnitude-only signal xm(n1,n2) by
![]() (1.43)
(1.43)
![]() (1.44)
(1.44)
where F-1[.] represents the inverse Fourier
transform operation. In phase-only signal synthesis, the correct phase is
combined with an arbitrary constant magnitude. In the magnitude-only signal
synthesis, the correct magnitude is combined with an arbitrary constant phase.
In this synthesis, ![]() often
preserves the intelligibility of
often
preserves the intelligibility of ![]() while
while ![]() does not. An example of this is shown in
Figure 1.31. Figure 1.31(a) shows an original image
does not. An example of this is shown in
Figure 1.31. Figure 1.31(a) shows an original image ![]() , and Figures 1.31(b) and (c)
show
, and Figures 1.31(b) and (c)
show ![]() and
and
![]() , respectively.
, respectively.

An experiment which more dramatically illustrates the
observation that phase-only signal synthesis captures more of the signal
intelligibility than magnitude-only synthesis can be performed as follows.
Consider two images ![]() and
and
![]() . From these
two images. we synthesize two other images
. From these
two images. we synthesize two other images ![]() and
and ![]() by
by
![]() (1.45)
(1.45)
![]() (1.46)
(1.46)
In this experiment, ![]() captures the intelligibility of
captures the intelligibility of ![]() , while
, while ![]() captures the
intelligibility of
captures the
intelligibility of ![]() .
An example is shown in Figure 1.32.
.
An example is shown in Figure 1.32.
Figures 1.32(a) and (b) show the two images ![]() and
and ![]() and Figures 1.32(c)
and (d) show the two images
and Figures 1.32(c)
and (d) show the two images ![]() and
and ![]() .
.

The high intelligibility of phase-only synthesis
raises the possibility of exactly reconstructing a signal ![]() from its Fourier transform
phase
from its Fourier transform
phase ![]() . This is known as the magnitude-retrieval problem. In fact,
it has been shown that a sequence
. This is known as the magnitude-retrieval problem. In fact,
it has been shown that a sequence ![]() is uniquely specified within a scale
factor if x(n1,n2) is real and has finite extent, and if
its Fourier transform cannot be factored as a product of lower-order
polynomials in
is uniquely specified within a scale
factor if x(n1,n2) is real and has finite extent, and if
its Fourier transform cannot be factored as a product of lower-order
polynomials in ![]() and
and ![]() . Typical images
. Typical images ![]() are real and have
finite regions of support. In addition, the fundamental theorem of algebra does
not apply to 2-D polynomials, and their Fourier transforms cannot generally be
factored as products of lower-order polynomials in
are real and have
finite regions of support. In addition, the fundamental theorem of algebra does
not apply to 2-D polynomials, and their Fourier transforms cannot generally be
factored as products of lower-order polynomials in ![]() and
and ![]() . Typical
images, then, are uniquely specified within a scale factor by the Fourier transform
phase alone.
. Typical
images, then, are uniquely specified within a scale factor by the Fourier transform
phase alone.
Two approaches to reconstructing a
sequence from its Fourier transform phase alone have been considered. The first
approach leads to a closed-form solution and the second to an iterative
procedure. In the first approach, ![]() is expressed as
is expressed as
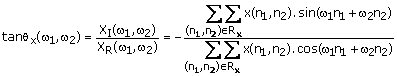 (1.47)
(1.47)
where Rx is the region of support of ![]() . Rewriting (1.47), we
have
. Rewriting (1.47), we
have
![]() (1.48)
(1.48)
Equation (1.48) is a linear equation for the unknown
values in ![]() for
each frequency
for
each frequency ![]() . If there are N2 unknown
values in
. If there are N2 unknown
values in ![]() ,
we can obtain a set of N2 linear equations for
,
we can obtain a set of N2 linear equations for ![]() by sampling
by sampling ![]() at N2
points. If the frequencies are sampled at distinctly different points,
noting that
at N2
points. If the frequencies are sampled at distinctly different points,
noting that ![]() is an odd function and is periodic with a period of 2p x 2p. The solution to the set
of N linear equations can be shown to be k
is an odd function and is periodic with a period of 2p x 2p. The solution to the set
of N linear equations can be shown to be k![]() , where k is an arbitrary real scaling
factor. An example of signal reconstruction from phase using (1.48) is shown in
Figure 1.33. Figure 1.33(a) shows an image of 16 x 16 pixels, and Figure
1.33(b) shows the reconstruction. The scaling factor of the reconstructed
sequence in the figure is chosen such that the reconstruction will match the
original sequence.
, where k is an arbitrary real scaling
factor. An example of signal reconstruction from phase using (1.48) is shown in
Figure 1.33. Figure 1.33(a) shows an image of 16 x 16 pixels, and Figure
1.33(b) shows the reconstruction. The scaling factor of the reconstructed
sequence in the figure is chosen such that the reconstruction will match the
original sequence.

The reconstruction algorithm discussed above is reasonable for a small size image, but is not practical for an image of typical size. For example, reconstructing an image of 512 x 512 pixels using (1.48) requires the solution of approximately a quarter of a million linear equations. An alternate approach is to recognize that the solution to the phase-only reconstruction problem must satisfy constraints in both the spatial and frequency domains. Specifically, the solution
· must be real,
· must be zero outside the known region of support, and
· must have a nonfactorable Fourier transform.
In addition, the phase of the Fourier transform of the
solution must be the same as the ![]() given. A useful
approach to solving such a problem is an iterative procedure, in which we
impose the spatial and frequency domain constraints separately in each domain.
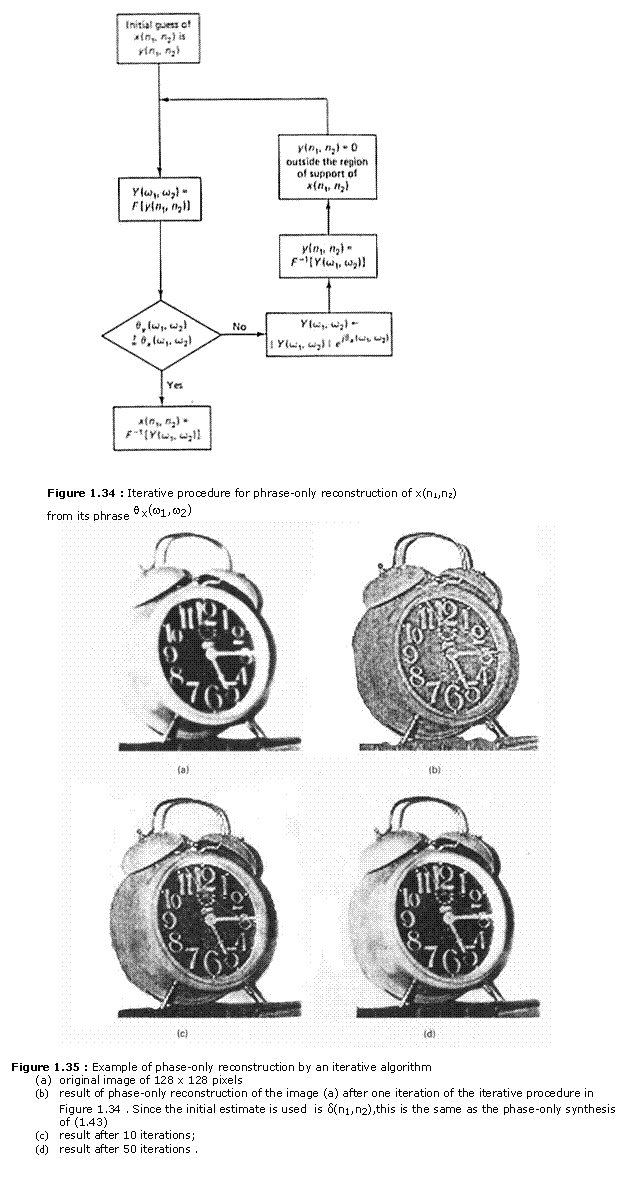
An iterative procedure for the phase-only reconstruction is shown in Figure
1.34. In the procedure, we begin with an initial estimate of the signal. This
can be any real sequence with the same region of support as x(n1,n2).
We next compute its Fourier transform. We then replace the Fourier transform
with the given
given. A useful
approach to solving such a problem is an iterative procedure, in which we
impose the spatial and frequency domain constraints separately in each domain.
An iterative procedure for the phase-only reconstruction is shown in Figure
1.34. In the procedure, we begin with an initial estimate of the signal. This
can be any real sequence with the same region of support as x(n1,n2).
We next compute its Fourier transform. We then replace the Fourier transform
with the given ![]() . The Fourier transform
magnitude is not affected. We then compute the inverse Fourier transform of the
modified Fourier transform. Due to the modification in the Fourier transform
domain, the sequence is no longer zero outside the known region of support of x(n1,n2).
We now impose the spatial domain constraint by setting the sequence to zero
outside the known region of support. The resulting sequence is a new estimate
of the solution. This completes one iteration in the iterative procedure. When
the initial estimate of the sequence chosen is real, the constraint that the
solution is real will automatically be satisfied. The above algorithm can be
shown to converge to the desired solution. An example of signal reconstruction
from phase using the iterative procedure in Figure 1 .34 is shown in Figure
1.35. Figure 1.35(a) shows an original imageof 128 x 128 pixels. Figures
1.35(b), (c), and (d) show the results of the iterative procedure after one
iteration [phase-only synthesis of (1.39)], 10 iterations, and 50 iterations.
The initial estimate used is d(n1,n2).
. The Fourier transform
magnitude is not affected. We then compute the inverse Fourier transform of the
modified Fourier transform. Due to the modification in the Fourier transform
domain, the sequence is no longer zero outside the known region of support of x(n1,n2).
We now impose the spatial domain constraint by setting the sequence to zero
outside the known region of support. The resulting sequence is a new estimate
of the solution. This completes one iteration in the iterative procedure. When
the initial estimate of the sequence chosen is real, the constraint that the
solution is real will automatically be satisfied. The above algorithm can be
shown to converge to the desired solution. An example of signal reconstruction
from phase using the iterative procedure in Figure 1 .34 is shown in Figure
1.35. Figure 1.35(a) shows an original imageof 128 x 128 pixels. Figures
1.35(b), (c), and (d) show the results of the iterative procedure after one
iteration [phase-only synthesis of (1.39)], 10 iterations, and 50 iterations.
The initial estimate used is d(n1,n2).
Although the magnitude-only
synthesis of (1.44) does not capture the intelligibility of typical signals,
almost all typical images are also uniquely specified by the Fourier transform
magnitude. Specifically, if x(n1,n2) is real, has finile
extent, and has a nonfactorable Fourier transform, then x(n1,n2)
is uniquely specified by its Fourier transform magnitude ![]() within
a sign factor, translation, and rotation by 180° degrees. This raises the
possibility of exactly reconstructing x(n1,n2) from
within
a sign factor, translation, and rotation by 180° degrees. This raises the
possibility of exactly reconstructing x(n1,n2) from ![]() within
a sign factor, translation and rotation by 180° degrees. This is known in
the literature as the phase-retrieval problem, and has many more
potential applications than the phase-only reconstruction problem.
Unfortunately, none of the algorithms developed to date are as straightforward
or well-behaved as the algorithms developed for the phase-only reconstruction
problem. It is possible to derive a closed-form algorithm or a set of linear
equations that can be used in solving for x(n1,n2) from
within
a sign factor, translation and rotation by 180° degrees. This is known in
the literature as the phase-retrieval problem, and has many more
potential applications than the phase-only reconstruction problem.
Unfortunately, none of the algorithms developed to date are as straightforward
or well-behaved as the algorithms developed for the phase-only reconstruction
problem. It is possible to derive a closed-form algorithm or a set of linear
equations that can be used in solving for x(n1,n2) from ![]() , but
their derivation is quite involved. In addition, the closed-form solution is
not practical for an image of reasonable size due to the large number of linear
equations that must be solved. It is also possible to derive an iterative
procedure similar to that in Figure 1.34, which was developed for the
phase-only reconstruction. The only modification required is to replace the
Fourier transform magnitude with the given
, but
their derivation is quite involved. In addition, the closed-form solution is
not practical for an image of reasonable size due to the large number of linear
equations that must be solved. It is also possible to derive an iterative
procedure similar to that in Figure 1.34, which was developed for the
phase-only reconstruction. The only modification required is to replace the
Fourier transform magnitude with the given ![]() rather than to replace
the Fourier transform phase with the given
rather than to replace
the Fourier transform phase with the given ![]() when the frequency
domain constraints are imposed. The algorithm has been observed to converge to
the desired solution when the initial estimate used is quite accurate or the
signal x(n1,n2) has a special characteristic such as a
triangular region of support. The magnitude-only reconstruction problem
specifies x(n1,n2) within a sign factor, translation, and
rotation by 180°, and, therefore, more than one solution is possible. Imposing an
initial estimate sufficiently close to a possible solution or imposing
additional constraints such as a triangular region of support appear to prevent
the iterative procedure from wandering around from one possible solution to
another, in general, however, the algorithm does not converge to the desired
solution. Figure 1.36 shows an example of signal reconstruction from the
magnitude using a closed-form algorithm. Figures 1.36(a) and (b) show the
original and the reconstruction respectively. Developing a practical procedure
that can be used to reconstruct x(n1,n2) from
when the frequency
domain constraints are imposed. The algorithm has been observed to converge to
the desired solution when the initial estimate used is quite accurate or the
signal x(n1,n2) has a special characteristic such as a
triangular region of support. The magnitude-only reconstruction problem
specifies x(n1,n2) within a sign factor, translation, and
rotation by 180°, and, therefore, more than one solution is possible. Imposing an
initial estimate sufficiently close to a possible solution or imposing
additional constraints such as a triangular region of support appear to prevent
the iterative procedure from wandering around from one possible solution to
another, in general, however, the algorithm does not converge to the desired
solution. Figure 1.36 shows an example of signal reconstruction from the
magnitude using a closed-form algorithm. Figures 1.36(a) and (b) show the
original and the reconstruction respectively. Developing a practical procedure
that can be used to reconstruct x(n1,n2) from ![]() remains
a problem for further research.
remains
a problem for further research.
