1.3.2  Examples

Example 1

  

  

  

  

  

  

  

  

  We wish to determine for the sequence h(n1,n2) shown in Figure 1.22(a). From (1.35).

  

  

                                                                  

 

 

  

  
 

  

  

              

  

  

  

  

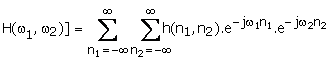
We knowthat          

  

And   therefore           and           can be written

  

  

      

  

  

 

 

  

The function for this example is real and its magnitude is sketched in Figure 1.22(b). If in Figure 1.22(b) is the frequency response of an LSI system the system corresponds to a lowpass filter. The function  shows smaller values   in frequency regions away from the origin. A lowpass filter applied to an image blurs the image. The function is 1 at  and therefore the average intensity of an image is not affected by the filter. A bright image will remain bright and a dark image will remain dark after processing with the filter. Figure 1.23(a) shows an image of pixels. Figure 1.23(b) shows the image obtained by processing the image in Figure 1.23(a) with a lowpass filter whose impulse response is given by h(n1,n2) in this example.

  

  

  

  

Example 2

  

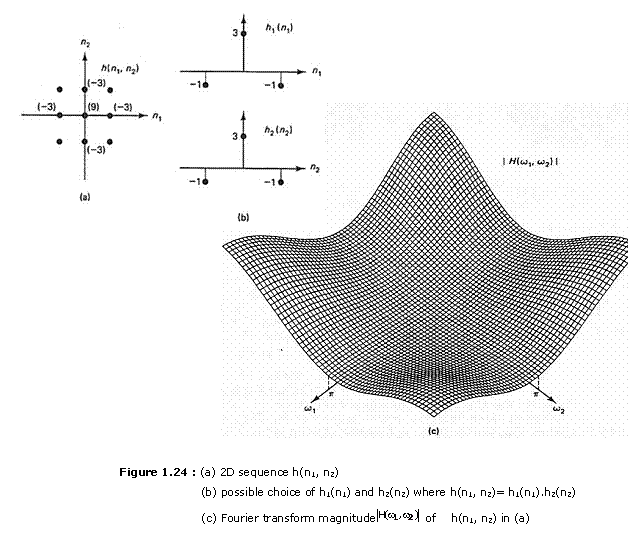
We wish to determine for the sequence h(n1,n2) shown in Figure 1.24(a). We can use (1.35) to determine , as in Example 1. Alternatively, we can use Property 4 in Table 1.1. The sequence h(n1,n2) can be expressed as h1(n1)h2(n2) where one possible choice of h1(n1) and h2(n2) is shown in Figure 1.24(b). Computing the 1-D Fourier transforms and and using Property 4 in Table 1.1. we have

  

  

    ,

  

Þ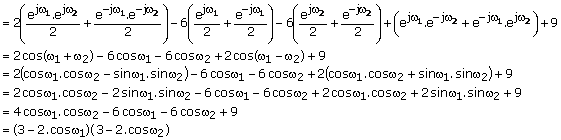 

  

  

  

  

The function is again real, and its magnitude is sketched in Figure 1.24(c). A system whose frequency response is given by the above is a highpass filter. The function has smaller values in frequency regions near the ori­gin. A highpass filter applied to an image tends to accentuate image details or local contrast. and the processed image appears sharper. Figure 1.25(a) shows an original image of pixels and Figure 1.25(b) shows the highpass filtered image using h(n1,n2) in this example. When an image is processed. for instance by highpass filtering, the pixel intensities may no longer he integers between 0 and 255. They may be negative, noninteger, or above 255. In such instances, we typically add a bias and then scale and quantize the processed image so that all the pixel intensities are integers between 0 and 255. It is common practice to choose the bias and scaling factors such that the minimum intensity is mapped to 0 and the maximum intensity is mapped to 255.

  

  

  

Example 3

  

  

  

  

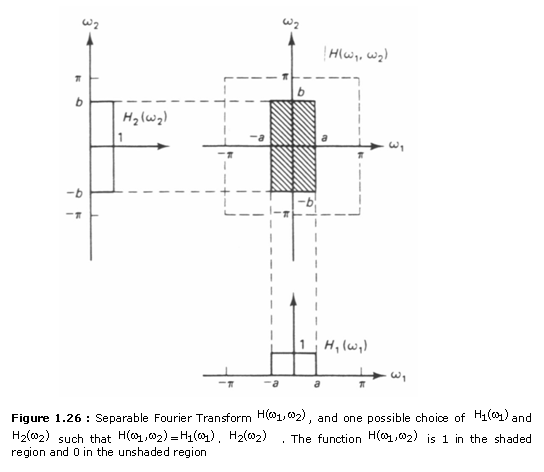
We wish to determine h(n1,n2) for the Fourier transform shown in Figure 1.23.    The function is given by

  

Since is always periodic with a period of 2∏ along each of the two variables and , is shown only for £ p and £ p.  The function can be expressed as H(o1) ., where one possible choice of and is also shown in Figure 1.26. When   above is the frequency response of a 2-D LSI system. the system is called a separable ideal lowpass filter. Computing the 1-D inverse Fourier transforms of and and using Property 4 in Table 1.1,we obtain;

  

We know by definition  that

  

      

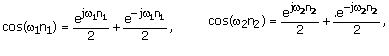
And also

=.     &      h(n1, n2) = h1(n1)h2(n2)

  

 

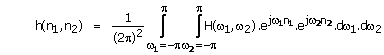
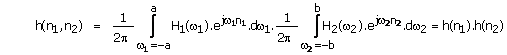
And therefore

  

  

  h(n1, n2) = h1(n1)h2(n2)= 

  

  

  

  

Example 4

  

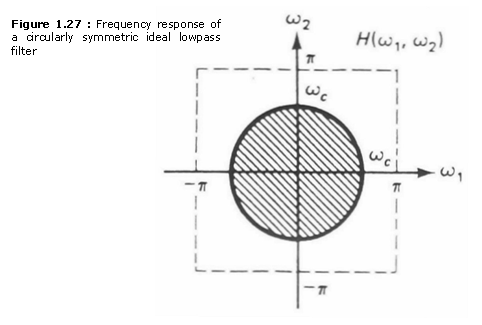
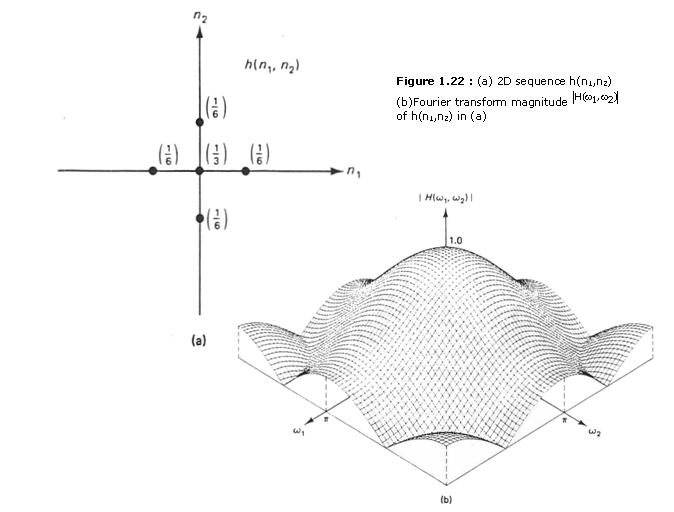
We wish to determine h(n1, n2) for the Fourier transform shown in Figure 1.27. The function is given by

                 

  

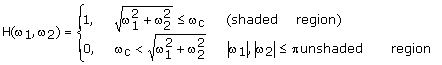
When above is the frequency response of a 2-D LSI system, the system is called a circularly symmetric ideal lowpass filter, or an ideal lowpass filter for short. The inverse Fourier transform of in this example requires a fair amount of algebra. The result is

                                                              h                                          (1.40)

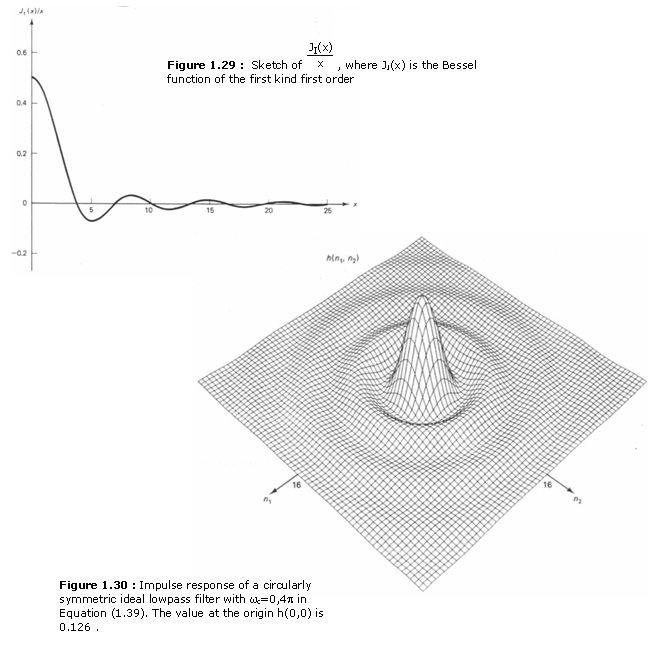
where represents the Bessel function of the first kind and the first order and can be expanded in series form as

                                                                             (1.41)

  

This example shows that 2-D Fourier transform or inverse Fourier transform opera­tions can become much more algebraically complex than 1-D Fourier transform or inverse Fourier transform operations, despite the fact that the 2-D Fourier transform pair and many 2-D Fourier transform properties are straightforward extensions of 1-D results. From (1.40). we observe that the impulse response of a 2-D circularly sym­metric ideal lowpass filter is also circularly symmetric, that is, it is a function of . This is a special case of a more general result. Specifically, if is a function of in the region and is a constant outside the region, then the corresponding h(n1, n2) is a function of . Note, however, that circular symmetry of h(n1, n2) does not imply circular symmetry of . The function is sketched in Figure 1.28. The sequence h(n1, n2) in (1.40) is sketched in Figure 1 .29 for the case = 0.4∏.

The impulse responses h(n1, n2) obtained from the separable and circularly symmetric ideal lowpass filters in Examples 3 and 4 above are not absolutely sum-

mable, and their Fourier transforms do not converge uniformly to used to obtain h(n1, n2). This is evident from the observation that the two contain discontinuities and are not analytic functions. Nevertheless, we will regard them as valid Fourier transform pairs, since they play an important role in digital filtering and the Fourier transforms of the two h(n1, n2) converge to in the mean square sense.