1.3.2 Properties

    We can derive a number of useful properties from the Fourier transform pair in (1.35). Some of the more important properties, often useful in practice, are listed in Table 1.1. Most are essentially straightforward extensions of 1-D Fourier transform properties. The only exception is Property 4, which applies to separable sequences. If a 2-D sequence x(n₁, n₂) can be written as x₁(n₁)x₂(n₂), then its Fourier transform, is given by X₁(w₁)X₂(w₂), where X₁(w₁) and X₂(w₂) represent the 1-D Fourier transforms of x₁(n₁) and x₂(n₂) respectively. This property follows directly from the Fourier transform pair of (1 .35). Note that this property is quite different from Property 3, the multiplication property. In the multiplication property, both x(n₁, n₂) and y(n₁, n₂) are 2-D sequences. in Property 4, x₁(n₁) and x₂(n₂) are 1-D sequences, and their product x₁(n₁)x₂(n₂) forms a 2-D sequence.

TABLE 1.1  :  PROPERTIES OF FOURIER TRANSFORM                   

Property 1. Linearity

Property 2. Convolution

Property 3. Multiplication

Property 4. Separable Sequence

Property 5. Shift of a Sequence and a Fourier Transform

(a).

(b)

Property 6. Differentiation

(a)

               (b) 

Property 7. Initial Value and DC Value Theorem

(a)

(b)   

Property 8. Parseval’s Theorem

              (a)   

              (b)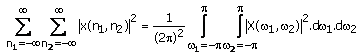

Property 9. Symmetry Properties

(a)

                (b)

                (c)

(d)

(e)

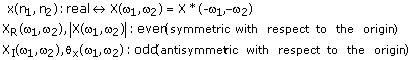
(f)

              (g)

Property 10. Uniform Convergence

For a stable x(n₁,n₂) the Fourier transform of h(n₁,n₂) uniformly converges.