1.3 THE FOURIER TRANSFORM
1.3.1 The Fourier Transform Pair
It is a remarkable fact that any stable sequence x(n1,
n2) can be obtained by appropriately combining complex exponentials
of the form ![]() .The
function
.The
function ![]() ,which
represents the amplitude associated with the complex exponential
,which
represents the amplitude associated with the complex exponential ![]() ,can be obtained from
x(n1, n2). The relationships between x(n1, n2)
and
,can be obtained from
x(n1, n2). The relationships between x(n1, n2)
and ![]() are
given by
are
given by
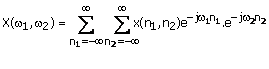 (1.35a)
(1.35a)
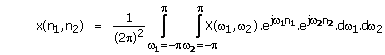 (1.35b)
(1.35b)
![]()
![]()
![]() (1.35c)
(1.35c)
Equation (1.35a) shows how the amplitude ![]() associated with the exponential
associated with the exponential
![]() can
be determined from x(n1, n2). The function
can
be determined from x(n1, n2). The function ![]() is called the
discrete-space Fourier transform, or Fourier transform for short, of x(n1,
n2). Equation (1.31b) shows how complex exponentials
is called the
discrete-space Fourier transform, or Fourier transform for short, of x(n1,
n2). Equation (1.31b) shows how complex exponentials ![]() are specifically
combined to form x(n1, n2). The sequence x(n1,
n2) is called the inverse discrete-space Fourier transform
or inverse Fourier transform of
are specifically
combined to form x(n1, n2). The sequence x(n1,
n2) is called the inverse discrete-space Fourier transform
or inverse Fourier transform of ![]() . The consistency of (1.31a) and (1.31b)
can be easily shown by combining them.
. The consistency of (1.31a) and (1.31b)
can be easily shown by combining them.
From (1.35), it can be seen that ![]() is in general complex, even
though x(n1, n2) may be real. It is often convenient to
express
is in general complex, even
though x(n1, n2) may be real. It is often convenient to
express ![]() in
terms of its magnitude
|
in
terms of its magnitude
|![]() | and phase
| and phase ![]() or in terms
of its real part
or in terms
of its real part ![]() and
imaginary part
and
imaginary part ![]() as
as
![]() (1.36)
(1.36)
From (1.35), it can also be seen that ![]() is a function of
continuous variables w1 and w2, although x(n1, n2) is a function of discrete
variables n1 and n2 . In addition,
is a function of
continuous variables w1 and w2, although x(n1, n2) is a function of discrete
variables n1 and n2 . In addition, ![]() is always periodic with a
period of 2∏ x 2∏ ; that is,
is always periodic with a
period of 2∏ x 2∏ ; that is, ![]() for all w1 and w2. We can also show that the Fourier
transform converges uniformly for stable sequences. The Fourier transform of
x(n1, n2) is said to converge uniformly when
for all w1 and w2. We can also show that the Fourier
transform converges uniformly for stable sequences. The Fourier transform of
x(n1, n2) is said to converge uniformly when ![]() is finite and
is finite and
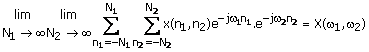 for all w1 and w2
(1.37)
for all w1 and w2
(1.37)
When the Fourier transform of x(n1, n2)
converges uniformly, ![]() is an analytic function and is
infinitely differentiable with respect to w1 and w2.
is an analytic function and is
infinitely differentiable with respect to w1 and w2.
A sequence x(n1, n2)
is said
to be an eigenfunction of a system T if T[x(n1, n2)]=k.x(n1,
n2) for some scalar k. Suppose we use a complex exponential ![]() as an input
x(n1, n2) to an LSI system with impulse response h(n1,
n2). The output of the system y(n1, n2) can be
obtained as
as an input
x(n1, n2) to an LSI system with impulse response h(n1,
n2). The output of the system y(n1, n2) can be
obtained as
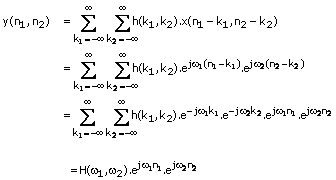 (1.38)
(1.38)
From (1.38), ![]() is an eigenfunction of any LSI system
for which
is an eigenfunction of any LSI system
for which ![]() is well defined and
is well defined and ![]() is the Fourier
transform of h(n1,n2). The function
is the Fourier
transform of h(n1,n2). The function ![]() is
called the frequency response of the LSI system. The fact that
is
called the frequency response of the LSI system. The fact that ![]() is an
eigenfunction of an LSI system and that
is an
eigenfunction of an LSI system and that ![]() is the scaling
factor by which
is the scaling
factor by which ![]() is
multiplied when it is an input to the LSI system simplifies system analysis
for a sinusoidal input. For example. the output of an LSI system with frequency
response
is
multiplied when it is an input to the LSI system simplifies system analysis
for a sinusoidal input. For example. the output of an LSI system with frequency
response ![]() when the input is
when the input is ![]() can be obtained as
follows:
can be obtained as
follows:
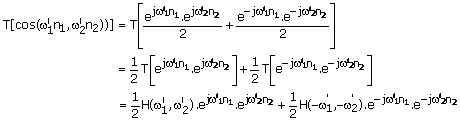 (1.39)
(1.39)