1.2.3 Stable Systems and Special Support Systems
For practical reasons, it is often appropriate to impose additional constraints on the class of systems we consider. Stable systems and special support systems have such constraints.
Stable systems. A system is considered stable in the bounded-input-bounded-output (BIBO) sense if and only if a bounded input always leads to a bounded output. Stability is often a desirable constraint to impose, since an unstable system can generate an unbounded output, which can cause system overload or other difficulties. From this definition and (1.18), it can be shown that a necessary and sufficient condition for an LSI system to be stable is that its impulse response h(n1, n2) be absolutely summable:
Stability of an
LSI system Û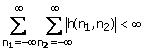 
(1.33)
Although (1.33) is a straightforward extension of 1-D results, 2-D systems differ greatly from 1-D systems when a system’s stability is tested. Because of (1.33), an absolutely summable sequence is defined to be a stable sequence. Using this definition, a necessary and sufficient condition for an LSI system to be stable is that its impulse response be a stable sequence.
Special support systems. A 1-D system is said to be causal if and only if the current output y(n) does not depend on any future values of the input, for example, x(n + 1), x(n + 2), x(n + 3),…… Using this definition, we can show that a necessary and sufficient condition for a 1-D LSI system to be causal is that its impulse response h(n) be zero for n <0. Causality is often a desirable constraint to impose in designing 1-D systems. A noncausal system would require delay, which is undesirable in such applications as real time speech processing. in typical 2-D signal processing applications such as image processing, the causality constraint may not be necessary. At any given time, a complete frame of an image may be available for processing, and it may be processed from left to right, from top to bottom, or in any direction one chooses. Although the notion of causality may not be useful in 2-D signal processing, it is useful to extend the notion that a 1-D causal LSI system has an impulse response h(n) whose nonzero values lie in a particular region. A 2-D LSI system whose impulse response h(n1, n2) has all its nonzero values in a particular region is called a special support system.
A 2-D LSI system is said to be a quadrant support system when its impulse response h(n1, n2) is a quadrant support sequence. A quadrant support sequence, or a quadrant sequence for short, is one which has all its nonzero values in one quadrant. An example of a first-quadrant support sequence is the unit step sequence u(n1, n2).
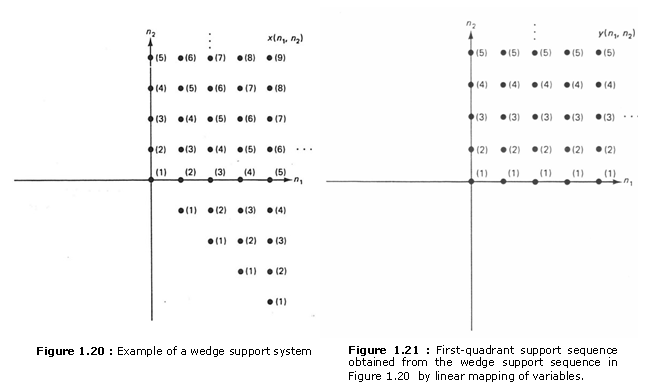
A 2-D LSI system is said to be a wedge support system when its impulse response h(n1, n2) is a wedge support sequence. Consider two lines emanating from the origin. If all the nonzero values in a sequence lie in the region hounded by these two lines, and the angle between the two lines is less than 180o. the sequence is called a wedge support sequence. or a wedge sequence for short. An example of a wedge support sequence x(n1, n2) is shown in Figure 1.20.
Quadrant support sequences and wedge support sequences arc closely related. A quadrant support sequence is always a wedge support sequence. In addition. it can be shown that any wedge support sequence can always he mapped to a first-quadrant support sequence by a linear mapping of variables without affecting its stability. To illustrate this, consider the wedge support sequence x(n1, n2) shown in Figure 1.20. Suppose we obtain a new sequence v(n1, n2) from x(n1, n2) by the following linear mapping of variables:
(1.34)
where the integers l1,l2,l3,and l4 are chosen to be 1, 0, -1 and 1 respectively. The sequence y(n1, n2) obtained by using (1.34) is shhhhhhown in Figure 1.21 and is clearly a first-quadrant support sequence. In addition, the stability of x(n1, n2) is equivalent to the stability of y(n1, n2), since
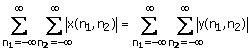
The notion that a wedge support sequence can always he transformed to a first-quadrant support sequence by a sim pie linear mapping of variables without affecting its stability is very useful in studying the stability of a 2-D system. Our primary concern in testing the stability of a 2-D system will be limited to a class of systems known as recursively computable systems. To test the stability of a recursively computable system, we need to test the stability of a wedge support sequence h’(n1, n2). To accomplish this, we will transform h’(n1, n2) to a first-quadrant support sequence h” (n1, n2) by an appropriate linear mapping of variables and then check the stability of h” (n1, n2). This approach exploits the fact that it is much easier to develop stability theorems for first-quadrant support sequences than for wedge support sequences.
