1.2.1 Linear Systems and Shift-Invariant Systems
This
definition of a system is very broad.
Only in very special circumstances do our systems analysis problems
become mathematically tractable. To make any progress at all, we must restrict
the class of systems which we will consider. Without any restrictions, characterizing
a system requires a complete input-output relationship. Knowing the output of a
system to one set of inputs does not generally allow us to determine the output
of the system to any other set of inputs. Two types of restriction which
greatly simplify the characterization and analysis of a system are linearity
and shift invariance. In practice, fortunately, many systems can be
approximated to be linear and shift invariant.
The linearity of a system T is defined as ;
Linearity Û T[ax1(n1, n2) +
bx2(n1, n2] = ay1(n1,
n2) + by2(n1, n2) (1.12)
where
T[x1(n1, n2]
= y1(n1, n2), T[x2(n1, n2)]
= y2(n1, n2)
a and b are any scalar constants, and
AÛB means that A implies B and B implies A. The
condition in (1.12) is called the principle of superposition. To
illustrate this concept, a linear system and a nonlinear system are shown in
Figure 1.13(a).
Suppose we first apply
x1(n1, n2) as the input and find that
y1(n1, n2) as the response. Now what would happen if we had
used ax1(n1, n2) + bx2(n1,
n2) as the
input where a and b are constants? In general, if the system is not linear, the
response to this combination or superposition of inputs could be quite
arbitrary. But a linear system has the defining property that the superposition
of inputs ax1(n1, n2)
+ bx2(n1, n2) produces an output which is a
corresponding superposition ay1(n1, n2) + by2(n1,
n2). By definition this property must hold for any x1(n1,
n2), x2(n1, n2), a, and b.
The
shift invariance (SI) or space invariance of a system is defined
as
Shift-invarianceÛ T[x(n1-m1, n2 - m2)]
= y(n1 - m1, n2 - m2 ) (1.13)
where
y(n1,
n2) = T[x(n1, n2)] and m1 and
m2 are any integers.
A system is shift-invariant if it
has the property that system behaviour does not
depend on where the input is applied. More precisely, if we know that y(n1, n2) is the response to x(n1, n2), then the
defining property of the space-invariant system is that y(n1 - m1, n2 -
m2 ) is the response to x(n1 - m1, n2 -
m2 ) where m1 and m2
are any constants. We insist that this property be true for any
choice of x(n1, n2) and
m1 , m2 .
For convenience refer to Figure
1.13(b).
In the example above in
Figure 1.13 (a) there is a system T .
What can we say about the systems ;
·
linearity?
·
shift-invariance ?
Is the system linear
?
The system T is given as ;
y(n1, n2)=T[x(n1, n2)]= x(n1, n2) . g(n1, n2)
The principle of superposition
(linearity rule) is
given as ;
T[ax1(n1, n2)
+ bx2(n1, n2] = ay1(n1,
n2) + by2(n1, n2)
Then ;
T[x(n1, n2)]= x(n1, n2) . g(n1, n2)
T[ax1(n1, n2) + bx2(n1,
n2] = [ax1(n1, n2) + bx2(n1,
n2]. g(n1,
n2) (Expression-a)
and
y(n1, n2)=
x(n1, n2)
. g(n1, n2)
ay1(n1, n2) + by2(n1,
n2)= [ax1(n1, n2). g(n1, n2)] +
[bx2(n1, n2). g(n1, n2)]
= [ax1(n1, n2)
+ bx2(n1, n2)]. g(n1, n2) (Expression-b)
Expression-a ® T[ax1(n1,
n2) + bx2(n1, n2] = [ax1(n1,
n2) + bx2(n1, n2]. g(n1, n2)
Expression-b ® ay1(n1,
n2) + by2(n1, n2)= [ax1(n1,
n2) + bx2(n1, n2)]. g(n1,
n2)
As Expression-a=Expression-b the rule of linearity is satisfied and the
system is said to be linear.
Now let’s look if the system is shift-invariant ?
The system T is given as ; y(n1, n2)=T[x(n1, n2)]=
x(n1, n2)
. g(n1, n2)
Shift-invariance rule : T[x(n1-m1,
n2 - m2)] = y(n1 - m1, n2 -
m2 )
T[x(n1, n2)]= x(n1, n2) . g(n1,
n2)
T[x(n1-m1,
n2 - m2)] = x(n1-m1, n2 - m2) . g(n1,
n2) (Expression-c)
and
y(n1,
n2)= x(n1,
n2) . g(n1, n2)
y(n1 - m1, n2 -
m2 )= x(n1-m1,
n2 - m2) . g(n1-m1, n2 -
m2) (Expression-d)
As Expression-c ¹ Expression-d the rule of shift-invariance is not satisfied and
the system is said to be not shift-invariant
or other words the system is shift-variant.
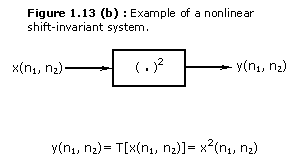
In the example above in Figure 1.13
(b) there is a system T. What can we say
about the systems ;
·
linearity?
·
shift-invariance ?
Is the system linear
?
The system T is given as ;
y(n1, n2)= T[x(n1,
n2)]= x2(n1, n2)
The principle of superposition
(linearity rule) is
given as ;
T[ax1(n1, n2) + bx2(n1,
n2)] = ay1(n1, n2) +
by2(n1, n2)
Then ;
If input x(n1, n2) can be written as the sum of two other
functions such as x1(n1,
n2) + x2(n1, n2)
x(n1, n2) = x1(n1, n2)
+ x2(n1, n2)
Then we have to say that the square of the input is equal to
square of the sum such as ;
x2(n1, n2)=[
x1(n1, n2) + x2(n1, n2)]2
If
T[x(n1, n2)]= x2(n1,
n2) then
T[ax1(n1, n2) + bx2(n1,
n2)]= )=[ x1(n1, n2) + x2(n1,
n2)]2 (Expression-a)
On the other hand ;
y(n1, n2)= x2(n1,
n2)
From property the definition we know
that
y1(n1, n2) =
T[x1(n1, n2)]
which makes y1(n1,
n2) = x12(n1, n2)
Same as y1(n1,
n2) we can write
Y2(n1, n2) = T[x2(n1,
n2)]= x22(n1, n2)
Therefore
ay1(n1, n2) +
by2(n1, n2)=ax12(n1,
n2)+bx22(n1, n2) (Expression-b)
Expression-a ® T[ax1(n1,
n2) + bx2(n1, n2] = [ax1(n1,
n2) + bx2(n1, n2]2
Expression-b ® ay1(n1,
n2) + by2(n1, n2)= ax12(n1,
n2) + bx22(n1, n2)
We see that Expression-a ¹ Expression-b and the system is not linear and said to
be non-linear.
Now let’s look if the system is shift-invariant ?
The system T is given as ; y(n1, n2)=T[x(n1, n2)]=
x2(n1, n2)
Shift-invariance rule : T[x(n1-m1,
n2 - m2)] = y(n1 - m1, n2 -
m2 )
T[x(n1, n2)]= x2(n1, n2)
T[x(n1-m1,
n2 - m2)] = x2(n1-m1, n2 - m2) (Expression-c)
and
y(n1,
n2)= x2(n1, n2)
y(n1 - m1, n2 -
m2 )= x2(n1-m1, n2 - m2) (Expression-d)
As Expression-c = Expression-d the rule of shift-invariance is satisfied and the
system is said to be shift-invariant.
Consider a linear system T.
Using (1.2) and (1.12). we can express the output y(n1,
n2) for an input x(n1, n2) as
x(n1, n2) =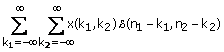
and (1.12),
T[ax1(n1, n2) + bx2(n1,
n2] = ay1(n1, n2) +
by2(n1, n2)
we can express the output y(n1,
n2) for an input x(n1, n2) as
(1.14)
From (1.14), a linear system can be
completely characterized by the response of the system to the impulse d(n1, n2) and
its shifts d(n1 - k1, n2
- k2). If we know T[d(n1 — k1, n2
— k,)] for all integer values of k1 and k2 the output of the linear system to any input
x(n1, n2) can be
obtained from (1.14). For a nonlinear system. knowledge of T[d(n1-k1,n2-k2)]
for all integer values of k1 and k2 does not tell us the
output of the system when the input x(n1,n2) is 2d(n1, n2), d(n1, n2) +d(n1-1, n2), or
many other sequences.
System characterization is further simplified if we impose the
additional restriction of shift-invariance. Suppose we denote the response of
a system T to an input d(n1, n2) by h(n1, n2);
h(n1, n2) = T[d(n1, n2)]. (1.15)
From (1.13)
T[x(n1-m1, n2 - m2)]
= y(n1 - m1, n2 - m2 )
and (1.15), we can write
h(n1 — k1, n2 — k2) = T[d(n1 — k1,n2 —
k2)] (1.16)
for a shift-invariant system T. For a
linear and shift-invariant (LSI) system, then from (1.14) and (1.16), the
input-output relation is given by
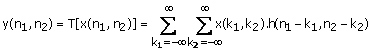(1.17)
Equation (1.17) states that an LSI
system is completely characterized by the impulse response h(n1,
n2) Specifically, for an LSI system, knowledge of h(n1,
n2) alone allows us to determine the output of the system to
any input from (1.17). Equation (1.17) is referred to as convolution, and is
denoted by the convolution operator “*“ as follows:
For an LSI system.
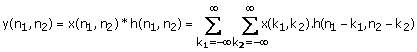(1.18)
Note that the impulse response h(n1, n2) which plays such an
important role for an LSI system, loses its significance for a nonlinear or
shift-variant system. Note also that an LSI system can be completely
characterized by the system response to one of many other input sequences. The
choice of d(n1, n2) as
the input in characterizing an LSI system is the simplest both conceptually and
in practice.