1.1.1 Examples of Sequences

Certain sequences and classes of  sequences play a particularly important role in 2-D signal processing. These are

· impulses,

· step sequences,

· exponential sequences,

· separable sequences,  and

· periodic sequences.

Impulses        ;

The impulse or unit sample sequence, denoted by d(n₁,n₂) is defined as  ;

                   (1.1)

The sequence d(n₁,n₂) , sketched in Figure 1.4 plays a similar role to the impulse d(n) in 1-D signal processing.

Figure 1.4 : Impulse d(n₁,n₂).

Any sequence x(n₁,n₂) can be represented as a linear combination of shifted impulses as follows

x(n₁,n₂)=.......+ x(-1,-1) . d(n₁+1,n₂+1) + x(0,-1) . d(n₁,n₂+1) + x(1,-1) . d(n₁-1,n₂+1)

· ....+ x(-1,0) . d(n₁+1,n₂) + x(0,0) . d(n₁,n₂) + x(1,0) . d(n₁-1,n₂)

+.....+ x(-1,1) . d(n₁+1,n₂-1) +..........................

=                                 (1.2)

Line impulses constitute a class of impulses which do not have any counterparts in 1-D. An example of line impulse is the 2-D sequence d_T(n₁) , which is sketched in Figure 1.5 and is defined as ;

                 (1.3)

Another example for line impulse is d_T(n₂)

Another example for line impulse is d_T((n₁ - n₂)

Step Sequences   ;

The unit step sequence , denoted by u(n₁,n₂)

                                                                           (1.4)

The sequence  u(n₁,n₂) , which is sketched in Figure 1.6 , is related to d_T(n₁,n₂) as

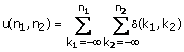                                                                        (1.5a)

or

                      (1.5b)

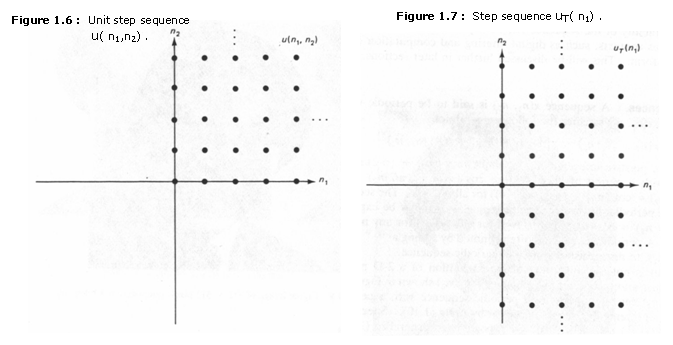
Some step sequences have no counterparts in 1-D. An example is the 2-D sequence d_T(n₁) , which is sketched in Figure 1.7 and is defined as

                                                               (1.6a)

Other examples include d_T(n₂) and d_T(n₁-n₂) , which are defined similarly to d_T(n₁).

                                                                         (1.6b)

and

                                                      (1.6c)

Exponential Sequences   ;

Exponential sequences are of the type are important for system analysis

Separable Sequences    ;

A 2-D sequence x(n₁,n₂) is said to be a separable sequence if it can be expressed as

x(n₁,n₂) = f(n₁) . g(n₂)                                                        (1.7)

where f(n₁) is a function of only n₁ and g(n₂) is a function of only n_{2 .} Although it is posible to view f(n₁) and  g(n₂) as 2-D sequences , it is more convenient to consider them to be 1-D sequences . For that reason, wwe use the notations  f(n₁)  and   g(n₂)  , rather than f_T(n₁)   and  g_T(n₂).

The impulse d(n₁,n₂)  can be expressed as

d(n₁,n₂)= d(n₁) . d(n₂)                                                  (1.8)

where d(n₁) and  d(n₂)  are 1-D impulses. The unit step sequence u(n₁,n₂)  is also a separable sequence since  u(n₁,n₂)  can be expressed as

u(n₁,n₂)=u(n₁) . u(n₂)                                                         (1.9)

where   u(n₁)  and  u(n₂)  are 1-D unit step sequence. Another example  of a separable sequence is

which can be written as .

Separable sequences form a very special class of  2-D sequences. A typical 2-D sequence is not a separable sequence. As an illustration, consider a sequence x(n₁,n₂)  which is ;

A general sequence x(n₁,n₂) of this type has N₁N₂ degrees of freedom. If x(n₁,n₂) is a separable sequence, x(n₁,n₂) is completely specified by some   f(n₁)  which is zero outside 0 £n₁£ N₁-1  and some g(n₂) which is zero outside 0 £n₂£ N₂-1  and consequently has only N₁ + N₂ degrees of freedom.

Despite the fact that separable sequences constitute a very special class of 2-D sequences, they play an important role in 2-D signal processing. In those cases where the results that apply to 1-D sequences do not expand to general 2-D sequences in a straightforward manner,they often do for separable 2-D sequences.

Periodic Sequences   ;

A sequence x(n₁, n₂) is said to be periodic with a period of N₁ x N₂ if x(n₁, n₂) satisfies the following condition:

x(n₁, n₂) = x(n₁ + N₁, n₂) = x(n₁, n₂ + N₂)     for all (n₁, n₂)                         (1.10)

where N₁ and N₂ are positive integers.

For example, cos (∏n₁+∏ n₂) is a periodic sequence with a period of 2 x 4, since

for all (n₁,n₂).

The sequence cos (n₁ + n₂) is not periodic, however, since cos (n₁ + n₂) cannot be expressed as cos ((n₁ + N₁) + n₂) = cos (n₁ + (n₂ + N₂)) for all (n₁,n₂)  for any nonzero integers N₁ and N₂.  A periodic sequence is often denoted by adding a “~” (tilde). For example, , to distinguish it from an aperiodic sequence.

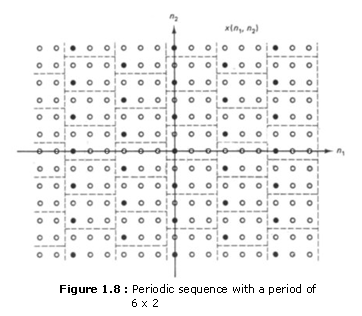
Equation (1.10) is not the most general representation of a 2-D periodic sequence. As an illustration, consider the sequence x(n₁,n₂) shown in Figure 1.8. Even though x(n₁, n₂) can be considered a periodic sequence with a period of 3 x 2 it cannot be represented as such a sequence by using (1.10). Specifically. x(n₁,n₂) ¹ x(n₁ + 3, n₂) for all (n₁,n₂). It is possible to generalize (1.10) to incorporate cases such as that in Figure 1.8. However, we will use (1.10) to define a periodic sequence, since it is sufficient for our purposes, and sequences such as that in Figure 1.8 can be represented by (1.10) by increasing N₁ and/or N₂. For example, the sequence in Figure 1.8 is periodic with a period of 6 x 2 using (1.10).