1.1 SIGNALS
The signals we consider are discrete-space signals. A 2-D discrete-space signal (sequence) will be denoted by a function whose two arguments are integers. For example; x(n1,n2) represents a sequence (digital signal) which is defined for all integer values of n1 and n2 . Note that x(n1,n2) for non-integer n1 and n2 are not zero, but is undefined. The notation x(n1,n2) may refer either to the discrete-space function x or to the value of the x at a specific (n1,n2).
An example of 2-D sequence x(n1,n2) is sketched in Figure 1.1 . In the figure, the height at (n1,n2) represents the amplitude at (n1,n2) . An alternative way to sketch the 2-D sequence in Figure 1.1 is shown in Figure 1.2 . In this figure open cicles representsamplitudes of 0 and filled-in circles represent non-zero amplitudes, with the values in parentheses representing the amplitudes . For example ; x(3,0) is 0 and x(1,1) is 2 , x(-1,0) is 2, x(-1,-2)is 1.
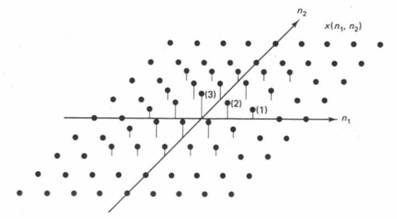
Figure 1.1 : 2-D sequence (digital signal) x(n1,n2)
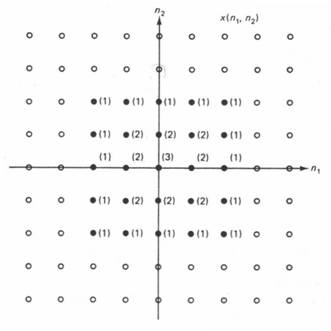
Figure 1.2 : Alternative way to sketch the 2-D sequence in Figure 1.1. Open circles represent amplitudes of zero, and filled-in circles represent non-zero amplitudes, with values in parentheses representing the amplitude.
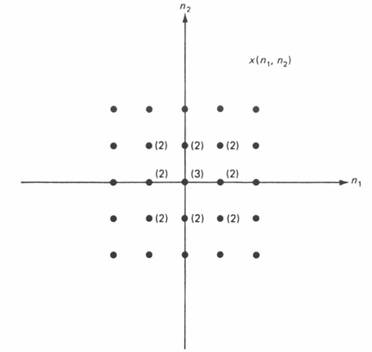
Figure 1.3 : Sequence in Figure 1.2 sketched with some simplification. Open circles have been eliminated and filled-in circles with amplitude of 1 have no amplitude specifications.